Проецирование точки в начертательной геометрии с примерами. Методы проецирования в начертательной геометрии с примерами
- Проецирование точки в начертательной геометрии с примерами. Методы проецирования в начертательной геометрии с примерами
- Центральное проецирование. Центральное проецирование
- Проецирование точки онлайн. Проекция вектора
- Проецирование точки инженерная графика. Проецирование точки на две плоскости проекций
- Горизонтальная проекция точки. Проецирование точки в начертательной геометрии с примерами
- Проекция точки по координатам. Построение проекций точки
- Как построить на плоскости проекцию точки. Проекция точки на плоскость. Проекция точки на прямую на плоскости
Проецирование точки в начертательной геометрии с примерами. Методы проецирования в начертательной геометрии с примерами
проецированием.
В начертательной геометрии для решения геометрических задач используется графический способ, при котором геометрические свойства предметов изучаются непосредственно по чертежу'. Для того, чтобы чертеж соответствовал изображаемому предмету, он должен быть построен по определенным геометрическим законам. Правила построения изображений в начертательной геометрии основаны на методе проекции. Метод проекций предполагает наличие плоскости проекций, объекта проецирования и проецирующих лучей.
Принятые обозначения:
Обозначения геометрических фигур
1. Точки, расположенные в пространстве,обозначаются прописными буквами латинского алфавита
2. Последовательность точек(и других элементов) - подстрочными индексами:
3. Линии в пространстве- по точкам, определяющим линию или строчными буквами латинского алфавита:
4. Углы- строчными буквами греческого алфавита
5. Плоскости- строчными буквами греческого алфавита
6. Поверхности- римскими цифрамиа также прописными буквами русского алфавита: цилиндр -конус - сфера -
7. Плоскости проекций- строчной буквой греческого алфавита Произвольная плоскость - горизонтальная - фронтальная -профильная - любая дополнительная -
8. Оси проекций- строчными буквамиили (при введении дополнительных плоскостей) Начало координат - прописной буквой
9. Проекции точек:
- на произвольную плоскость
- на горизонтальную плоскость
- на фронтальную плоскость
- на профильную плоскость
- на дополнительную плоскость
10. Проекции линий- по проекциям точек, определяющих линию; кроме того:
- горизонтальная линия - буквой
- фронтальная линия - буквой
- профильная линия - буквой
11. Обозначение плоскостей, заданных следами:
- горизонтальный след плоскости
- фронтальный след плоскости
- профильный след плоскости
В тех случаях, когда плоскость не требует наименования, обозначение следов упрощенно -
Для проецирующих плоскостей задаётся проекция плоскости:
- - горизонтально - проецирующая плоскость
- - фронтально - проецирующая плоскость
- - профильно - проецирующая плоскость
Точки схода следов плоскости - прописными буквами X, Y, Z с индексом соответствующей плоскости: Xtt, Ya, Ztt.
12. При преобразовании эпюра (чертежа) вращением(или совмещением) в новом положении:
- точки -
- плоскости -
- следы плоскости -
После второго вращения соответственно:
Новое положение точки схода следов при вращении плоскости
Обозначения отношений между геометрическими элементами
1. Совпадение
- точкиисовпадают.
2. Параллельность ():
- прямые ипараллельны.
3. Перпендикулярность
- Прямаяперпендикулярна плоскости
Обозначения теоретико-множественные
1. Принадлежность ();
- точкапринадлежит прямой.
2. Включение ():
- прямая a принадлежит плоскости
3. Пересечение ():
- точкаесть пересечение прямойс плоскостью
4. Импликация - логическое следствие
- еслиипараллельны прямой то они параллельны между собой.
В начертательной геометрии, как правило, используются графический способ для решения геометрических задач. Для этого геометрические свойства объектов изучаются непосредственно по чертежу. Чтобы чертеж соответствовал изображаемому предмету, он должен быть построен по определенным геометрическим законам. Метод проекций основан на существовании плоскости проекций, объекта проецирования и проецирующих лучей. Это позволяет получать изображения, которые отображают геометрические свойства объектов. В начертательной геометрии используются следующие обозначения:Обозначения геометрических фигур
В тех случаях, когда плоскость не требует наименования, обозначение следует упрощать.Проецирующие плоскости
Для проецирующих плоскостей задается проекция плоскости: * Точки схода следов плоскости - прописными буквами X, Y, Z с индексом соответствующей плоскости: Xtt, Ya, Ztt. * Новое положение точки схода следов при вращении плоскости.Обозначения отношений между геометрическими элементами
Совпадение
* точки - точки совпадают.Параллельность
* прямые - параллельны.Перпендикулярность
* прямая - перпендикулярна плоскостиОбозначения теоретико-множественные
Принадлежность
* точка - принадлежит прямой.Включение
* прямая a - принадлежит плоскостиПересечение
* точка - есть пересечение прямой с плоскостьюИмпликация
* если - параллельны прямая, то они параллельны между собой. Примеры использования этих обозначений: * Если прямая и прямая параллельны, то они параллельны между собой. * Точка - принадлежит прямой, если она лежит на ней. * Плоскость - включает прямую, если она лежит на ней. Таким образом, обозначения и методы проецирования в начертательной геометрии позволяют получать точные и понятные изображения геометрических объектов, что является важным шагом в решении геометрических задач.Центральное проецирование. Центральное проецирование
Проецирование (лат. Projicio – бросаю вперёд) – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.
Центральное проецирование заключается в проведении через каждую точку ( А, В, С ,…) изображаемого объекта и определённым образом выбранный центр проецирования ( S ) прямой линии ( SA , SB , >… — проецирующего луча ).
Введём следующие обозначения (Рисунок 1.1):
S – центр проецирования (глаз наблюдателя);
π1 – плоскость проекций;
A, B, C – объекты проецирования – точки;
SA , SB – проецирующие прямые (проецирующие лучи).
Примечание : левой клавишей мыши можно переместитьКРАСНУЮточку в горизонтальной плоскости, при щелчке на точке левой клавишей мыши, изменится направление перемещения и её можно будет переместить по вертикали.
Центральной проекцией точки называется точка пересечения проецирующей прямой, проходящей через центр проецирования и объект проецирования (точку), с плоскостью проекций.
Свойство 1 . Каждой точке пространства соответствует единственная проекция, но каждой точке плоскости проекций соответствует множество точек пространства, лежащих на проецирующей прямой.
Докажем это утверждение.
На рисунке 1.1: точка А 1– центральная проекция точки А на плоскости проекций π1. Но эту же проекцию могут иметь все точки, лежащие на проецирующей прямой. Возьмём на проецирующей прямой SA точку С . Центральная проекция точки С ( С 1) на плоскости проекций π1 совпадает с проекцией точки А ( А 1):
- С ∈ SA ;
- SC ∩ π1= C 1 → C 1 ≡ A 1.
Следует вывод, что по проекции точки нельзя судить однозначно о её положении в пространстве.
Чтобы устранить эту неопределенность, т.е. сделать чертеж обратимым , введём еще одну плоскость проекций (π2) и ещё один центр проецирования ( S 2) (Рисунок 1.2).
Рисунок 1.2 – Иллюстрация 1-го и 2-го свойств
Построим проекции точки А на плоскости проекций π2. Из всех точек пространства только точка А имеет своими проекциями А 1 на плоскость π1 и А 2 на π2 одновременно. Все другие точки лежащие на проецирующих лучах будут иметь хотя бы одну отличную проекцию от проекций точки А (например, точка В ).
Свойство 2 . Проекция прямой есть прямая.
Докажем данное свойство.
Соединим точки А и В между собой (Рисунок 1.2). Получим отрезок АВ , задающий прямую. Треугольник Δ SAB задает плоскость, обозначенную через σ. Известно, что две плоскости пересекаются по прямой: σ∩π1= А 1 В 1, где А 1 В 1 – центральная проекция прямой, заданной отрезком АВ .
Метод центрального проецирования – это модель восприятия изображения глазом, применяется главным образом при выполнении перспективных изображений строительных объектов, интерьеров, а также в кинотехнике и оптике. Метод центрального проецирования не решает основной задачи, стоящей перед инженером – точно отразить форму, размеры предмета, соотношение размеров различных элементов.
Проецирование точки онлайн. Проекция вектора
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:Прab = |b|cos(a,b) или
где a•b -,|a|- модуль вектораa.Инструкция . Для нахождения проекции вектораПpabв онлайн режиме необходимо указать координаты векторовaиb. При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word . Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
Классификация проекций вектора
Виды проекций по определению проекция вектора
- Геометрическая проекция вектора AB на ось (вектор) называется вектор A'B' , начало которого A’ есть проекция начала A на ось (вектор), а конец B’ – проекция конца B на ту же ось.
- Алгебраическая проекция вектора AB на ось (вектор) называется длина вектора A'B' , взятая со знаком+или-, в зависимости от того, имеет ли вектор A'B' то же направление, что и ось (вектор).
Виды проекций по системе координат
- проекции на плоскости (система координат OX,OY). Пример: a (2;-3), a =2i-3j
- проекции в пространстве (система координат OX,OY, OZ). Пример: a (2;-3;1), a =2i-3j+k
- проекции в N-мерном пространстве
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.AC' = AB' + B'C'
Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:Прab = |b|·cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак. |
| Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак. |
| Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB. |
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор). |
Проецирование точки инженерная графика. Проецирование точки на две плоскости проекций
Образование отрезка прямой линии АА 1 можно представить как результат перемещения точки А в какой-либо плоскости Н (рис. 84, а), а образование плоскости — как перемещение отрезка прямой линии АВ (рис. 84, б).
Рис. 84
Точка — основной геометрический элемент линии и поверхности, поэтому изучение прямоугольного проецирования предмета начинается с построения прямоугольных проекций точки.
В пространство двугранного угла, образованного двумя перпендикулярными плоскостями — фронтальной (вертикальной) плоскостью проекций V и горизонтальной плоскостью проекций Н, поместим точку A (pre. 85, а).
Линия пересечения плоскостей проекции ' V и Н — прямая, которая называется осью проекций и обозначается буквой х.
Плоскость V здесь изображена в виде прямоугольника, а плоскость Н — в виде параллелограмма. Наклонную сторону этого параллелограмма обычно проводят под углом 450 к его горизонтальной стороне. Длина наклонной стороны берется равной 0,5 ее действительной длины.
Из точки А опускают перпендикуляры на плоскости V и Н. Тогда а ' и а пересечения перпендикуляров с плоскостями проекций V и Н являются прямоугольными проекциями точки А. Фигура А ааха' в пространстве — прямоугольник. Сторона аах этого прямоугольника на наглядном изображении уменьшается в 2 раза.
Совместим плоскости Н с плоскостью V, вращая V вокруг линии пересечения плоскостей x . В результате получается комплексный чертеж точки A (рис. 85, б).
Для упрощения комплексного чертежа границы плоскостей проекций V и Н не указывают (рис. 85, в).
Перпендикуляры, проведенные из точки А к плоскостям проекций, называются проецирующими линиями, а основания этих проецирующих линий — точки а и а' — называются проекциями точки A : а' — фронтальная проекция точки А. а — горизонтальная проекция точки А.
Линия а'а называется вертикальной линией проекционной связи.
Рис. 85
Расположение проекции точки на комплексном чертеже зависит от положения этой точки в пространстве.
Если точка А лежит на горизонтальной плоскости проекций Н (рис. 86, а), то ее горизонтальная проекция а совпадает с заданной точкой, а фронтальная проекция а' располагается на оси х. При расположении точки В на фронтальной плоскости проекций V ее фронтальная проекция совпадает с этой точкой, а горизонтальная проекция лежит на оси х. Горизонтальная и фронтальная проекции заданной точки С. лежащей па оси х, совпадают с этой точкой. Комплексный чертеж точек А, В и С показан на рис. 86, б.
Горизонтальная проекция точки. Проецирование точки в начертательной геометрии с примерами
Если из точки , находящуюся в пространстве, относительно двух плоскостей проекций
Они характеризуются координатами, которые численно равны расстоянию от точки до соответствующих плоскостей проекций. Координаты обозначаются теми же буквами, что и оси вдоль которых измеряется расстояние, с присвоением индекса самой буквы.
Так, для точки :
Плоскость прямоугольника, перпендикулярна к: оси x, а линии пересечений плоскостей и плоскости являются прямыми и , перпендикулярными к оси х.
Изображение точки и её проекций на рис.3.1 является пространственным чертежом, что не всегда удобно для практики.
Рис. 2.4 Чтобы получить плоский чертёж, поворачивают плоскость, вокруг оси и совмещают её с плоскостью (рис. 3.1), получая таким образом. комплексный чертеж (эпюр Монжа)
Проекции и оказываются на одной линии, которая называется линией проекционной связи. Она перпендикулярна к оси х (рис. 3.2). При проецировании точки А на три плоскости проекций от плоскости она отстоит на расстоянии (рис. 3.3). При этом, аналогично вышесказанному:
Для получения плоского чертежа в этом случае уже две плоскостиисовмещаются с плоскостьюпутём поворота их соответственно вокруг осей и . При этом ось у как бы раздваивается (как бы разрезается вдоль), и положение плоскостей будет таким, как показано на рис. 3.3. Профильная проекция точки находится на пересечении линий связи и (расстояние ).
Перенос точки в точку ( ) - понятен из чертежа, а сам отрезок есть не что иное, как координата .
На плоском трёхмерном чертеже положительное направление оси совпадает с отрицательным направлением оси , а отрицательное направление оси - с положительным направлением оси .
Это не означает, что модули этих величин обязательно равны между собой, т.е. (в частном случае это равенство может быть). Те же рассуждения будут справедливы и в отношении направлений осей и (рис. 3.4).
Таким образом, горизонтальная и фронтальная проекции точки на плоском чертеже лежат на одной линии проекционной связи, перпендикулярной к оси , а фронтальная и профильная проекции точки на линии проекционной связи, перпендикулярной к оси
Определение по плоскому чертежу принадлежности точки тому или другому октанту пространства
Точка, например
- II или VI октанту, если иилежат над осью х ;
- III или VII октанту, еслилежит над осью х , а- под осью х ;
- IV или VIII октанту, если иилежат под осью х .
Определение по плоскому чертежу принадлежности точки плоскостям проекций
Точка А
Любая точка лежит на оси проекций, если её смежные две проекции совпадают.
Проекция точки по координатам. Построение проекций точки
Для изображения точки, находящейся в пространстве, необходимо взять три взаимно перпендикулярные плоскости: горизонтальную ( H ), фронтальную ( V ) и профильную ( W ). На ортогональном чертеже они изображаются осями проекций ОХ, ОУ, ОZ . Точку на чертеже можно построить по трем координатам Х (абсцисса), У (ордината), Z (аппликата).
Например, построим точку А с координатами Х = 60 мм, У = 40 мм, Z = 70 мм (рис. 91). Задание записывается следующим образом:
А (60, 40, 70). Координаты точки всегда задаются в одинаковой последовательности: Х, У, Z . Размеры даются в миллиметрах.
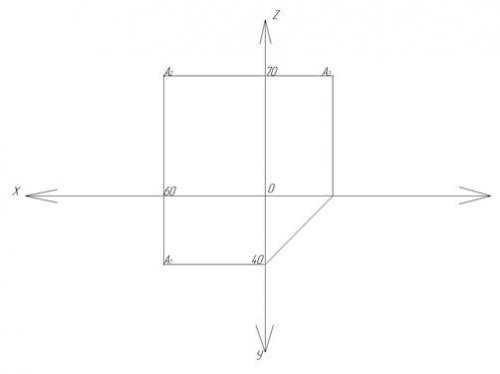
Рис. 91. Построение точки А по координатам
на ортогональном чертеже
Существует восемь четвертей пространства, которые называются октантами. Задачи в начертательной геометрии обычно задаются в первом октанте, где значения координат Х, У, Z положительные. Но существуют октанты, где значения координат отрицательные. На рисунке 92 показаны, по каким осям откладываются отрицательные и положительные значения координат точки.

Рис. 92. Изображение осей с отрицательными
и положительными значениями координат
Задача 1
Построить три проекции точки с координатами В (-65, 30, -50). Определить, в каком октанте она находится.
Решение. Координата Х – отрицательная, значит, 65 мм отложим по оси Х справа от начала координат ( О ) (рис. 93). Проведем вертикальную проекционную связь. Так как знак координаты У положительный, отложим 30 мм от оси Х вниз по построенной проекционной связи, получим горизонтальную проекцию точки ( В1 ). Значение координаты Z отрицательное, следовательно, отложим 50 мм вниз от оси Х по той же проекционной связи, получим фронтальную проекцию точки ( В2 ).
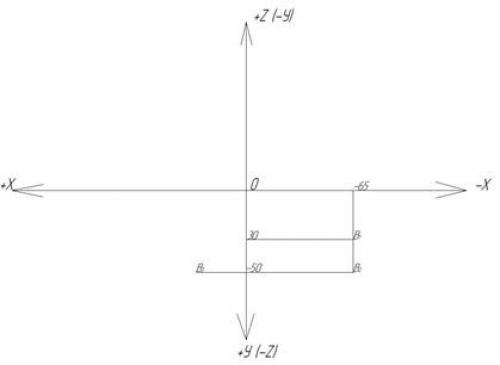
Рис. 93. Построение трех проекций точки В
Чтобы построить профильную проекцию точки, нужно взять значение координаты У и отложить его на горизонтальной проекционной связи, проведенной из фронтальной проекции В2 . Придерживаемся следующего правила: если значение У отрицательное, то его откладывают слева от оси координат; если значение У положительное, то его откладывают справа от оси координат.
Как построить на плоскости проекцию точки. Проекция точки на плоскость. Проекция точки на прямую на плоскости

Изучение свойств фигур в пространстве и на плоскости невозможно без знания расстояний между точкой и такими геометрическими объектами, как прямая и плоскость. В данной статье покажем, как находить эти расстояния, рассматривая проекцию точки на плоскость и на прямую.
Уравнение прямой для двумерного и трехмерного пространств

Расчет расстояний точки до прямой и плоскости осуществляется с использованием ее проекции на эти объекты. Чтобы уметь находить эти проекции, следует знать, в каком виде задаются уравнения для прямых и плоскостей. Начнем с первых.
Прямая представляет собой совокупность точек, каждую из которых можно получить из предыдущей с помощью переноса на параллельные друг другу вектора. Например, имеется точка M и N. Соединяющий их вектор MN¯ переводит M в N. Имеется также третья точка P. Если вектор MP¯ или NP¯ параллелен MN¯, тогда все три точки на одной прямой лежат и образуют ее.
В зависимости от размерности пространства уравнение, задающее прямую, может изменять свою форму. Так, всем известная линейная зависимость координаты y от x в пространстве описывает плоскость, которая параллельна третьей оси z. В связи с этим в данной статье будем рассматривать только векторное уравнение для прямой. Оно имеет одинаковый вид для плоскости и трехмерного пространства.
В пространстве прямую можно задать следующим выражением:
Здесь значения координат с нулевыми индексами соответствуют принадлежащей прямой некоторой точки, u¯(a; b; c) - координаты направляющего вектора, который лежит на данной прямой, α - произвольное действительное число, изменяя которое можно получить все точки прямой. Это уравнение называется векторным.
Часто приведенное уравнение записывают в раскрытом виде:
Аналогичным образом можно записать уравнение для прямой, находящейся в плоскости, то есть в двумерном пространстве:
Уравнение плоскости

Чтобы уметь находить расстояние от точки до плоскостей проекций, необходимо знать, как задается плоскость. Так же, как и прямую, ее можно представить несколькими способами. Здесь рассмотрим один единственный: общее уравнение.
Предположим, что точка M(x0; y0; z0) плоскости принадлежит, а вектор n¯(A; B; C) ей перпендикулярен, тогда для всех точек (x; y; z) плоскости справедливым будет равенство:
Следует запомнить, что в этом общем уравнении плоскости коэффициенты A, B и C являются координатами нормального к плоскости вектора.
Расчет расстояний по координатам
Перед тем как переходить к рассмотрению проекций на плоскость точки и на прямую, следует напомнить, как следует рассчитывать расстояние между двумя известными точками.
Пусть имеются две пространственные точки:
Тогда дистанция между ними вычисляется по формуле:
С помощью этого выражения также определяют длину вектора A1A2¯.
Для случая на плоскости, когда две точки заданы всего парой координат, можно записать аналогичное равенство без присутствия в нем члена с z:
Теперь рассмотрим различные случаи проекции на плоскости точки на прямую и на плоскость в пространстве.
Точка, прямая и расстояние между ними
Предположим, что имеется некоторая точка и прямая:
Расстояние между этими геометрическими объектами будет соответствовать длине вектора, начало которого лежит в точке P2, а конец находится в такой точке P на указанной прямой, для которой вектор P2P ¯ этой прямой перпендикулярен. Точка P называется проекцией точки P2на рассматриваемую прямую.
Ниже приведен рисунок, на котором изображена точка P2, ее расстояние d до прямой, а также вектор направляющий v1¯. Также на прямой выбрана произвольная точка P1и от нее до P2проведен вектор. Точка P здесь совпадает с местом, где перпендикуляр пересекает прямую.

Видно, что оранжевые и красные стрелки образуют параллелограмм, сторонами которого являются вектора P1P2¯ и v1¯, а высотой - d. Из геометрии известно, что для нахождения высоты параллелограмма следует разделить его площадь на длину основания, на которое опущен перпендикуляр. Поскольку площадь параллелограмма вычисляется как векторное произведение его сторон, то получаем формулу для расчета d:
Все вектора и координаты точек в этом выражении известны, поэтому можно им пользоваться без выполнения каких-либо преобразований.
Решить эту задачу можно было бы иначе. Для этого следует записать два уравнения:
- скалярное произведение P2P ¯ на v1¯ должно равняться нулю, поскольку эти вектора взаимно перпендикулярны;
- координаты точки P должны удовлетворять уравнению прямой.
Этих уравнений достаточно, чтобы найти координаты P, а затем и длину d по формуле, приведенной в предыдущем пункте.