Взаимное расположение точек и прямой. Геометрия 7 класс. Точка, прямая и отрезок

Взаимное расположение точек и прямой. Геометрия 7 класс. Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Запомните!

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

В тексте точку обозначают символом « (·)» . Принадлежность и непринадлежность точки прямой обозначают символами « ∈ » и « ∉ ». Знак принадлежности можно запомнить как зеркальное отображение буквы « Э » или как знак евро « € » .

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

• (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a );
• (·)G ∈ a — точка G принадлежит прямой a ;
• (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a );
• (·)H ∉ a — точка H не принадлежит прямой a .

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

На рисунке изображены:
• Прямая a
• Прямая f
• Прямая CH
• Прямая DK

Точки D, E и F — лежат на одной прямой, поэтому: прямая DE , прямая EF и прямая DF — это три разных имени одной и той же прямой.

Разбор примера

Проведите прямую, обозначьте её буквой a и отметьте точки A и B , лежащие на этой прямой, и точки P, Q и R , не лежащие на ней. Опишите взаимное расположение точек A, B, P, Q, R и прямой a , используя символы ∈ и ∉ .

Решение задачи

Проведём прямую.

Обозначим её буквой a .

Опишем взаимное расположение точек и прямой.

• (·)A ∈ a
• (·)B ∈ a
• (·)P ∉ a
• (·)Q ∉ a
• (·)R ∉ a

Задача решена.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Взаимное расположение прямых и плоскостей в пространстве. Взаимное расположение прямых в пространстве

Если рассматривать две прямые на плоскости, то они либо не пересекаются, либо пересекаются только в одной точке. Те прямые, которые не пересекаются и лежат в одной плоскости, называют параллельными . А те, которые пересекаются, имеют особое название только в одном случае - если пересекаются под прямым углом. Такие прямые называются перпендикулярными .

Существуют ли в пространстве прямые, которые пересекаются и которые не пересекаются? Ответ на этот вопрос дают образы окружающего мира. Имеют ли такие прямые свое название и как их различать - вы узнаете из этого параграфа.
По аксиоме стереометрии, если две прямые пересекаются, то через них можно провести единственную плоскость. Это означает, что любые две пересекающиеся прямые определяют плоскость, а плоскости, в свою очередь, - пространство.

Итак, в пространстве прямые, расположенные в одной плоскости, могут пересекаться или быть параллельными. По аксиоме параллельных прямых, через точку вне прямой можно провести единственную прямую, параллельную данной. По следствию из аксиомы стереометрии, через прямую и точку вне ее можно провести единственную плоскость. Поэтому выходит, что две параллельные прямые задают плоскость.

Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются.

Если две произвольные прямые

Рассмотрим модель куба, изготовленного из «проволочных отрезков», лежащих на соответствующих прямых (рис. 3.1). Среди прямых, на которых лежат ребра куба, есть такие, которые не пересекаются и лежат в одной плоскости (и,и,ии т.д.), т.е. являются параллельными, однако есть и такие, которые не пересекаются и не являются параллельными (ииии т.д.). Такие прямые называются скрещивающимися .

Две прямые пространства, которые не пересекаются и не параллельны, называются скрещивающимися .

Понятно, что две скрещивающиеся прямые не могут лежать в одной плоскости. Поэтому говорят, что две прямые скрещиваются, если их нельзя поместить в одну плоскость. Для определения скрещивающихся прямых используют символ. Например(читается: «прямыеи- скрещивающиеся», или «прямаяскрещивается с прямой»). Особым случаем расположения прямых является их наложение - прямые совпадают.

Итак, расположение двух прямых в пространстве может быть следующим :

1. прямые пересекаются, если они имеют только одну общую точку;
2. прямые параллельны, если они не пересекаются и лежат в одной плоскости;
3. прямые скрещиваются, если они не пересекаются и не параллельны;
4. прямые совпадают, если они имеют хотя бы две общие точки.

Рассмотрим свойства, которыми обладают параллельные прямые в пространстве.

Теорема 1

Через любую точку пространства, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.

Доказательство:

Пустьпроизвольная прямая пространства,- точка, не принадлежащая ей (рис. 3.2). Через прямуюи точкуможно провести плоскость. Пусть это будет плоскость. На плоскостилежит прямая и точка вне ее. Через эту точку можно провести прямую, параллельную данной. Пусть прямаяи. Докажем, что прямаяединственная. Допустим, что существует другая прямая, которая не совпадает с прямой, параллельна прямойи проходит через точку. Поскольку, то по определению они лежат в одной плоскости, например.

Итак,и имеют общую прямую и точку, а поэтому совпадают. В плоскостичерез точкупроходят две прямые и, параллельные прямой, что противоречит аксиоме параллельности. Получили противоречие, которое доказывает единственность прямой, что и требовалось доказать. Теорема доказана .

Теорема 2 (признак параллельности прямых)

Если две прямые параллельны третьей прямой, то они параллельны между собой.

Доказательство:

Пусть прямыеипараллельны прямой с (рис. 3.3). Докажем, что прямыеипараллельны. Случай, когда прямые,, с лежат в одной плоскости, был рассмотрен в планиметрии. Это свойство еще называют признаком параллельности прямых. Поэтому будем считать, что эти прямые не лежат в одной плоскости, и докажем, что такой признак имеет место и в пространстве.
По условию, и поэтому эти прямые лежат в одной плоскости, пусть это будет плоскость. Аналогично, поэтому эти прямые будут лежать в некоторой другой плоскости - плоскости. Выберем на прямойточку. Через прямуюи точкупроведем плоскость, которая пересечет плоскостьпо некоторой прямой(иимеют общую точку). Поскольку через точкув плоскостиуже проходит прямая, то, т.е.пересекаетв некоторой точке, а значити. Однакопоэтому.
Т.е. точкапринадлежит трем плоскостями. Но все точки, общие для плоскостейи, лежат на прямой. Поэтому прямая а проходит через точку, что противоречит условию. Итак,не пересекает прямую, т.е.параллельна. Однако в плоскостичерез точкупроходит только одна прямая, параллельная прямой.

Взаимное расположение прямых в пространстве. Как выяснить взаимное расположение прямых в пространстве?

Рассмотрим две прямые пространства:

– прямую, заданную точкой и направляющим вектором;
– прямую, заданную точкой и направляющим вектором.

Для лучшего понимания выполним схематический чертёж: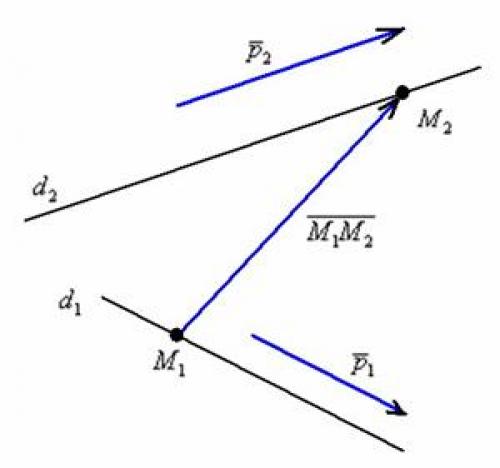
На чертеже в качестве примера изображены скрещивающиеся прямые.

Как разобраться с этими прямыми?

Так как известны точки, то легко найти вектор.

Если прямые скрещиваются , то векторы не компланарны(см. урок Линейная (не) зависимость векторов. Базис векторов ), а, значит, определитель, составленный из их координат, ненулевой. Или, что фактически то же самое, смешанное произведение векторов будет отлично от нуля:.

В случаях № 2-4 наша конструкция «падает» в одну плоскость, при этом векторы компланарны, а смешанное произведение линейно зависимых векторов равняется нулю:.

Раскручиваем алгоритм дальше. Предположим, что, следовательно, прямые либо пересекаются, либо параллельны, либо совпадают.

Если направляющие векторы не коллинеарны, то прямые пересекаются. Как проверить два вектора на коллинеарность, подробно рассмотрено в той же статье Линейная (не) зависимость векторов. Базис векторов .

Если направляющие векторы коллинеарны, то  прямые либо параллельны, либо совпадают. Финальным гвоздём предлагаю следующий приём: берём какую-либо точку одной прямой и подставляем её координаты в уравнение второй прямой; если координаты «подошли», то прямые совпадают, если «не подошли», то прямые параллельны.

Ход алгоритма незатейлив, но практические примеры всё равно не помешают:

Пример 11

Выяснить взаимное расположение двух прямых

Решение : как и во многих задачах геометрии, решение удобно оформить по пунктам:

1) Вытаскиваем из уравнений точки и направляющие векторы:

2) Найдём вектор:

Таким образом, векторы компланарны, а значит, прямые лежат в одной плоскости и могут пересекаться, быть параллельными или совпадать.

4) Проверим направляющие векторы на коллинеарность.

Составим систему из соответствующих координат данных векторов:

Из каждого уравнения следует, что, следовательно, система совместна, соответствующие координаты векторов пропорциональны, и векторы коллинеарны.

Вывод: прямые параллельны либо совпадают.

5) Выясним, есть ли у прямых общие точки. Возьмём точку, принадлежащую первой прямой, и подставим её координаты в уравнения прямой:

Таким образом, общих точек у прямых нет, и им ничего не остаётся, как быть параллельными.

Ответ :

Интересный пример для самостоятельного решения:

Пример 12

Выяснить взаимное расположение прямых

Обратите внимание, что у второй прямой в качестве параметра выступает буква. Логично. В общем случае – это же две различные прямые, поэтому у каждой прямой свой параметр.

Взаимное расположение точек в пространстве. Взаимное расположение точки, прямых и плоскостей с примерами

Взаимное расположение точки и прямой:

Возможны два варианта расположения точки относительно прямой:

• - точка принадлежит прямой (рис. 3.1 а), тогда ее проекции на КЧ лежат на одноименных проекциях прямой.
• - точка не принадлежит прямой (рис. 3.1 б), если хотя бы одна из проекций точки не принадлежит проекции прямой

Взаимное расположение прямых

Прямые в пространстве могут занимать друг к другу одно из трех положений:

• - быть параллельными;
• - пересекаться;
• - скрещиваться.

Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.

Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.

У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А . Причем фронтальная и горизонтальная проекции этой точки должны находиться на одной линии связи.

Рис. 3.3

Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.

Рис. 3.4

Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.

На рис. 3.4 точка С принадлежит прямой b , а точка D на прямой   а . Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций.

Плоскость. Способы ее задания, положение относительно плоскостей проекций

Положение плоскости в пространстве может быть однозначно определено:

• - тремя точками, не лежащими на одной прямой;
• - прямой и точкой, не лежащей на этой прямой;
• - двумя параллельными прямыми;
• - двумя пересекающимися прямыми;
• - плоской фигурой;
• - следом плоскости.

След плоскости – это линия пересечения заданной плоскости с одной из плоскостей проекций.

Соответственно различают горизонтальный, фронтальный и профильный следы плоскости.

Плоскостью общего положения называется плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций.

Плоскостями частного положения относительно плоскостей проекций называются плоскости параллельные или перпендикулярные им.

Плоскость перпендикулярная одной из плоскостей проекций называется проецирующей плоскостью.

Существует три вида проецирующих плоскостей: горизонтально- проецирующая, фронтально-проецирующая и профильно-проецирующая плоскости. Такие плоскости вырождаются в прямую линию (след плоскости) на ту плоскость проекций, к которой они перпендикулярны.

1. Горизонтально-проецирующая плоскость  - плоскость перпендикулярная горизонтальной плоскости проекций.

2. Фронтально-проецирующая плоскость – плоскость перпендикулярная фронтальной плоскости проекций.

3. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня.

Существует три вида плоскостей уровня: горизонтальная, фронтальная и профильная плоскости уровня.

1. Горизонтальная плоскость – плоскость, параллельная горизонтальной плоскости проекций.

2. Фронтальная плоскость  - плоскость, параллельная фронтальной плоскости проекций.

Взаимное расположение прямых на плоскости.. Простейшие задачи с прямой на плоскости. Взаимное расположение прямых. Угол между прямыми

Продолжаем рассматривать эти бесконечные-бесконечные прямые. На уроке Уравнение прямой на плоскости мы познакомились с основными видами уравнений, направляющим вектором прямой и её вектором нормали. Данная статья является логическим продолжением темы, и в ней будут разобраны следующие типовые задачи, для опытных путешественников сразу кликабельное оглавление:

О-о-о-о-о… ну и жесть, словновамсам себе приговор зачитал =) Впрочем, потом релаксация поможет, тем более, сегодня купил подходящие аксессуары. Поэтому приступим к первому разделу, надеюсь, к концу статьи сохраню бодрое расположение духа.

Взаимное расположение двух прямых

Рассмотрим две прямые, заданные уравнениями в общем виде:

Тот случай, когда зал подпевает хором. Две прямые могут :

1) совпадать;

2) быть параллельными:;

3) или пересекаться в единственной точке:.

Справка для чайников : пожалуйста, запомните математический знак пересечения , он будет встречаться очень часто. Запись обозначает, что прямая пересекается с прямой в точке.

Как определить взаимное расположение двух прямых?

Начнём с первого случая:

Две прямые совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны , то есть, существует такое число «лямбда», что выполняются равенства

Рассмотрим прямые и составим три уравнения из соответствующих коэффициентов:. Из каждого уравнения следует, что, следовательно, данные прямые совпадают.

Действительно, если все коэффициенты уравнения умножить на –1 (сменить знаки), и все коэффициенты уравнения сократить на 2, то получится одно и то же уравнение:.

Второй случай, когда прямые параллельны:

Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных пропорциональны:, но .

В качестве примера рассмотрим две прямые. Проверяем пропорциональность соответствующих коэффициентов при переменных:

Однако совершенно очевидно, что.

Вывод:

И третий случай, когда прямые пересекаются:

Две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных НЕ пропорциональны , то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства

Так, для прямых составим систему:

Из первого уравнения следует, что, а из второго уравнения:, значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных не пропорциональны.

Вывод: прямые пересекаются

В практических задачах можно использовать только что рассмотренную схему решения. Она, кстати, весьма напоминает алгоритм проверки векторов на коллинеарность, который мы рассматривали на уроке Понятие линейной (не) зависимости векторов. Базис векторов . Но существует более цивилизованная упаковка:

Пример 1

Выяснить взаимное расположение прямых:

Решение основано на исследовании направляющих векторов прямых:

а) Из уравнений найдём направляющие векторы прямых:.

Вычислим определитель, составленный из координат данных векторов:
, значит, векторы не коллинеарны и прямые пересекаются.

На всякий случай поставлю на распутье камень с указателями:

1) Если мало что понятно, начните со статьи Векторы для чайников .
2) Если не понятно, как находить направляющие векторы прямых, прошу посетить урок Уравнение прямой на плоскости .
3) Если неясно, причём тут определитель, вам сюда – Понятие линейной (не) зависимости векторов. Базис векторов .

Остальные перепрыгивают камень и следуют дальше, прямо к Кащею Бессмертному =)

б) Найдем направляющие векторы прямых:

Прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают. Тут и определитель считать не надо.

Очевидно, что коэффициенты при переменных пропорциональны, при этом.

Выясним, справедливо ли равенство:

Таким образом,

в) Найдем направляющие векторы прямых:

Вычислим определитель, составленный из координат данных векторов:
, следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают.

Коэффициент пропорциональности «лямбда» нетрудно усмотреть прямо из соотношения коллинеарных направляющих векторов. Впрочем, его можно найти и через коэффициенты самих уравнений:.

Теперь выясним, справедливо ли равенство. Оба свободных члена нулевые, поэтому:

Полученное значение удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).

Таким образом, прямые совпадают.

Взаимное расположение двух прямых. Взаимное расположения прямых на плоскости с примерами решения

Взаимное расположения прямых на плоскости:

Бывают два варианта взаимного расположения прямой и точки на плоскости: либо точка лежит на прямой в этом случае говорят, что прямая проходит через точку или точка не лежит на прямой иногда говорят, что точка не принадлежит прямой или прямая не проходит через точку.

Две прямые в плоскости могут пересекаться так как имеют общую точку или быть параллельными не имея общей точки. В пространстве может быть, когда две прямые не пересекаются, но они и не параллельны.

Определения

Два угла, на которые разбивается развернутый угол его внутренним лучом, называются смежными. Сумма мер двух: смежных углов равна 180°.

Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого угла Вертикальные углы равны.

Если две прямые пересекаются, они образуют четыре угла две пары вертикальных углов. Меньший из них — угол между данными прямыми.

Две прямые называются перпендикулярными, если они пересекаются под прямым углом. Отрезки или лучи называют перпендикулярными, если они лежат на перпендикулярных прямых Две прямые на плоскости называют параллельными, ест они не пересекаются.

Прямая, пересекающая две другие прямые, называется и: секущей. С двумя данными прямыми она образует 8 углов, не которые пары этих углов имеют отдельные названия:

• 1 и 3, 2 и 4 — внутренние накрест лежащие;
• 1 и 4,2 и 3 — внутренние односторонние;
• 1 и 8, 2 и 7, 3 и 6, 4 и 5 — соответственные;
• 5 и 7, 6 и 8 — внешние накрест лежащие;
• 5 и 8, 6 и 7 — внешние односторонние.

Признак параллельности прямых:

Две прямые параллельны, если с секущей они образу ют равные внутренние накрест лежащие углы, или равные соответственные углы, или такие внутренние одно сторонние углы, сумма которых равна 180°.

Свойства параллельных прямых:

Секущая с двумя параллельными прямыми образуя равные внутренние накрест лежащие углы, равные ее ответственные углы, такие внутренние односторонние углы, сумма которых равна 180°.

Две прямые, параллельные третьей, параллельны.

Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой прямо» Две прямые, перпендикулярные к третьей, параллельны

Смежные и вертикальные углы

Два угла, на которые делится развернутый угол его внутренним лучом, называют смежными.

Одна сторона у смежных углов общая, а две другие — дополнительные лучи. Если точки А, О, В лежат на одной прямой, а С — произвольная точка, не принадлежащая прямой АВ, то углы АОС и СОВ — смежные (рис. 45).

Свойство смежных углов сформулируем в виде теоремы.

В математике теоремой называют каждое утверждение, истинность которого устанавливается путем логических рассуждений. Цепочку таких рассуждений называют доказательством.

В нашем учебнике теоремы напечатаны жирным шрифтом и пронумерованы.

Теорема:   Сумма мер двух смежных углов равна 180°

Доказательство:

Объединение двух смежных углов является развернутым углом. Мера развернутого угла равна 180°. Значит, какими бы ни были смежные углы, сумма их мер равна 180°.

Два угла называются вертикальными, если стороны одного являются дополнительными лучами сторон другого. Например, если прямые АС и BD пересекаются в точке О, то углы AOD и ВОС — вертикальные (рис. 46). Каждый из них — смежный с углом АОВ. Углы АОВ и COD — тоже вертикальные.

Теорема: Вертикальные углы равны.

Доказательство:

Пусть AOD и ВОС — любые вертикальные углы (см. рис. 46). Каждый из них смежный с углом АОВ. По теореме о сумме смежных углов

отсюда 

Правые части этих равенств одинаковые, поэтому Что и следовало доказать 

Для любознательных:

Слово смежные употребляют не только применительно к углам. Смежный—это имеющий общую границу с чем-то или прилегающий к чему-то, соседний. Можно говорить о смежных комнатах, смежных полях и т. п. Относительно углов это понятие имеет особый смысл. Не каждые два угла с общей стороной называют смежными. Например, на рисунке 47 углы АОВ и ВОС имеют общую сторону ОВ, но не являются смежными.

Смежные углы — это два угла, состоящие в определенном отношении. Один угол не может быть смежным. Когда говорим, что какой-то угол смежный, то обязательно должны уточнить: смежный с каким углом? Отношение смежности углов имеет такое свойство: если угол А смежный с углом B, то и угол В смежный с углом А.