Точка и ее проекции. Разде. Предмет начертательной геометрии. Проецирование точки
- Точка и ее проекции. Разде. Предмет начертательной геометрии. Проецирование точки
- Точка принадлежит горизонтальной плоскости проекций. Прямая параллельная горизонтальной плоскости проекций п1
- Как построить на плоскости проекцию точки. Проецирование точки в начертательной геометрии с примерами
- Как построить проекцию точки. Взаимное положение двух точек. Условия видимости на чертеже
- Построить проекции точек по заданным координатам онлайн. Проекция вектора
- Проекция точки это. Проекция точки.
- Горизонтальная Проекция точки. Центральное проецирование
Точка и ее проекции. Разде. Предмет начертательной геометрии. Проецирование точки
1.1 Предмет начертательной геометрии
Начертательная геометрия (НГ) изучает методы изображения на плоскости пространственных объектов и алгоритмы решения позиционных, метрических и конструкторских задач. Под пространственными объектами следует понимать трехмерные объекты, т.е. имеющие три измерения – длину, ширину и толщину. Плоскость, как подсказывает здравый смысл, имеет два измерения (длину и ширину), если она ограничена. Позиционная задача – это задача на определение взаимного расположения геометрических объектов: за или перед объектом, слева или справа от него, сверху или снизу от него, какой из объектов видимый, какой – невидимый и др. Под метрическими понимаются задачи на определение действительных величин длин отрезков, углов наклона, плоских фигур, площадей и др. С этими пояснениями начальную формулировку предмета НГ следует понимать так. НГ – это наука, изучающая и устанавливающая методы изображения в двухмерном измерении трехмерных объектов и способы решения указанных выше задач.
Остается пояснить термин «конструкторские задачи». Под ними следует понимать задачи на принятие конкретного инженерного решения по осмыслению, изображению и созданию конкретного изделия, выраженного графическими методами.
В основу НГ положен метод проекций, т.е. точек, полученных пересечением проецирующих лучей с плоскостями проекций.
1.2 Наиболее употребительные теоретико-множественные символы и обозначения
А, В, С … a, b, c, l, m, n … , , , … Ф1, Ф2, … || .а , / | - - - - - - - - - - - - - | точка; линия; плоскость; поверхность; параллельность; перпендикулярность; скрещиваемость; «принадлежит», «содержится» (первый знак применяется по отношению к точке, второй – по отношению к множеству точек); знак отрицания, противоположности (эквивалентный отрицанию «не»); пересечение объектов (множеств); «отражает» (ся) «если … то»; обратимость («справедливо прямое и обратное утверждение»). |
Приведем несколько примеров, поясняющих применение символов.
l || m l || m a b m.n А l l А l А А (А l) (А l) (l m = K) (l m= K) | - - - - - - - - - - | прямая l параллельна прямой m. прямая l не параллельна прямой m. прямая a перпендикулярна прямой b. прямая m не параллельна и не пересекается с прямой n (т.е. они скрещивающееся). точка А принадлежит прямой l. прямая l принадлежит (содержится) в плоскости точка А не принадлежит прямой l. точка А отображается проекцией А(другими словами, проекция точки А есть точка А). если точка А принадлежит прямой l, то проекция Аточки А принадлежит проекции lпрямой l (обратное утверждение не всегда справедливо). |
Точка принадлежит горизонтальной плоскости проекций. Прямая параллельная горизонтальной плоскости проекций п1
Проекцией прямой, которая не перпендикулярна плоскости проекций, является прямая. Её положение определяется двумя точками, следовательно, для того чтобы построить проекцию прямой, достаточно построить проекции двух её точек.
Рисунок 8
а) Прямой общего положения называется прямая, которая не параллельна и не перпендикулярна ни одной из плоскости проекций. Пример такой прямой изображён на рисунке 8. Комплексный чертёж этой прямой будет выглядеть следующим образом.
Рисунок 9
б) Прямые частного положения – это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.
Первый подкласс прямых частного положения – прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.
Горизонталь – прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.
Рисунок 10
Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; α = Ð h П2.
Фронталь – прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.
Рисунок 11
Горизонтальная проекция фронтали параллельна оси Х, а угол β - угол наклона фронтали к горизонтальной плоскости проекций; f2// П2, β= Ð f1 П1.
Профильная прямая – это прямая, параллельная профильной плоскости П 3 . Комплексный чертёж профильной прямой изображён на рисунке 12. Горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси Х, а углы α и β - соответственно, углы наклона прямой к плоскостям П 1 и П2.
Рисунок 12.
Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.
Второй подкласс прямых частного положения – проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально–проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.
Их комплексные чертежи изображены соответственно на рисунке 13 (а, б, в).
Рисунок 13
Натуральная величина горизонтально-проецирующей прямой – её фронтальная проекция, фронтально-проецирующей прямой – её горизонтальная проекция, а профильно-проецирующей прямой – её горизонтальная и фронтальная проекции.
а) три точки, не лежащие на одной прямой;
Рисунок 14
б) прямая и точка, не лежащая на ней;
Рисунок 15
в) две параллельные прямые;
Рисунок 16
г) две пересекающиеся прямые;
Рисунок 17
д) плоская фигура (многоугольник, круг и т.д.).
Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Рисунок 18
Плоскости частного положения аналогично прямой подразделяются на плоскости уровня и проецирующие плоскости. На рисунке 19 (а,б,в) изображены, соответственно, горизонтальная, фронтальная и профильная плоскости. Причём горизонтальная плоскость задана двумя параллельными прямыми, фронтальная и профильная плоскости – двумя пересекающимися прямыми.
Рисунок 19
На рисунке 20 (а, б, в) показаны проецирующие плоскости. Горизонтально-проецирующая (рис. 20а) задана треугольником, фронтально-проецирующая (рис. 20б) - параллельными прямыми и профильно-проецирующая (рис. 20в) – пересекающимися прямыми.
Рисунок 20
1. Как образуется комплексный чертеж прямой линии?
Как построить на плоскости проекцию точки. Проецирование точки в начертательной геометрии с примерами
Если из точки , находящуюся в пространстве, относительно двух плоскостей проекций
Они характеризуются координатами, которые численно равны расстоянию от точки до соответствующих плоскостей проекций. Координаты обозначаются теми же буквами, что и оси вдоль которых измеряется расстояние, с присвоением индекса самой буквы.
Так, для точки :
Плоскость прямоугольника, перпендикулярна к: оси x, а линии пересечений плоскостей и плоскости являются прямыми и , перпендикулярными к оси х.
Изображение точки и её проекций на рис.3.1 является пространственным чертежом, что не всегда удобно для практики.
Рис. 2.4 Чтобы получить плоский чертёж, поворачивают плоскость, вокруг оси и совмещают её с плоскостью (рис. 3.1), получая таким образом. комплексный чертеж (эпюр Монжа)
Проекции и оказываются на одной линии, которая называется линией проекционной связи. Она перпендикулярна к оси х (рис. 3.2). При проецировании точки А на три плоскости проекций от плоскости она отстоит на расстоянии (рис. 3.3). При этом, аналогично вышесказанному:
Для получения плоского чертежа в этом случае уже две плоскостиисовмещаются с плоскостьюпутём поворота их соответственно вокруг осей и . При этом ось у как бы раздваивается (как бы разрезается вдоль), и положение плоскостей будет таким, как показано на рис. 3.3. Профильная проекция точки находится на пересечении линий связи и (расстояние ).
Перенос точки в точку ( ) - понятен из чертежа, а сам отрезок есть не что иное, как координата .
На плоском трёхмерном чертеже положительное направление оси совпадает с отрицательным направлением оси , а отрицательное направление оси - с положительным направлением оси .
Это не означает, что модули этих величин обязательно равны между собой, т.е. (в частном случае это равенство может быть). Те же рассуждения будут справедливы и в отношении направлений осей и (рис. 3.4).
Таким образом, горизонтальная и фронтальная проекции точки на плоском чертеже лежат на одной линии проекционной связи, перпендикулярной к оси , а фронтальная и профильная проекции точки на линии проекционной связи, перпендикулярной к оси
Определение по плоскому чертежу принадлежности точки тому или другому октанту пространства
Точка, например
- II или VI октанту, если иилежат над осью х ;
- III или VII октанту, еслилежит над осью х , а- под осью х ;
- IV или VIII октанту, если иилежат под осью х .
Определение по плоскому чертежу принадлежности точки плоскостям проекций
Точка А
Любая точка лежит на оси проекций, если её смежные две проекции совпадают.
Как построить проекцию точки. Взаимное положение двух точек. Условия видимости на чертеже
Рассмотрим чертеж модели, изображенной на рис. 3.6. Проекции некоторых точек совпадают, так как они расположены на одной проецирующей прямой. Например, на горизонтальной плоскости совпали проекции а и b вершин А и В - они лежат на одной горизонтально - проецирующей прямой. На фронтальной плоскости совпали проекции с ' и d ' вершин С и D - они лежат на одной фронтально-проецирующей прямой.
Точки, лежащие на одной проецирующей прямой, называют конкурирующими . А и В - горизонтально-конкурирующие точки, а С и D - фронтально-конкурирующие точки и т.д.
Ясно, что если две точки лежат на одной проецирующей прямой, то одна из них закрывает другую. Как определить, какая из них будет видимая и какая невидимая?
Из двух горизонтально- конкурирующих точек на горизонтальной плоскости видима та, которая расположена в пространстве выше. Анализируя положение фронтальных проекций точек (рис. 3.7), определяем, что точка А имеет большую координату z, чем точка В.
Следовательно, точка А расположена выше точки В и при проецировании на горизонтальную плоскость проекций закроет точку В. Точка А на горизонтальной плоскости видима, точка В - невидима. На фронтальной плоскости они обе видимы.
Из двух фронтально- конкурирующих точек на фронтальной плоскости проекций будет видима та, которая расположена ближе к наблюдателю, стоящему лицом к фронтальной плоскости проекций (рис. 3.8).
Какая из точек ближе к наблюдателю, можно определить по горизонтальным проекциям. Например, сравнивая горизонтальные проекции точек D и С , заключаем, что на фронтальной плоскости проекций видима точка С, а точка D - невидима, так как
Из двух профильно-конкурирующих точек на профильной плоскости проекций будет видима та точка, которая расположена левее.
Итак, если на чертеже одноименные проекции точек не совпадают или совпадает только одна пара проекций, то такие точки в пространстве не совпадают, а удалены друг от друга на определенное расстояние (рис. 3.7, 3.8).
Построить проекции точек по заданным координатам онлайн. Проекция вектора
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:Прab = |b|cos(a,b) или
где a•b -,|a|- модуль вектораa.Инструкция . Для нахождения проекции вектораПpabв онлайн режиме необходимо указать координаты векторовaиb. При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word . Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
Классификация проекций вектора
Виды проекций по определению проекция вектора
- Геометрическая проекция вектора AB на ось (вектор) называется вектор A'B' , начало которого A’ есть проекция начала A на ось (вектор), а конец B’ – проекция конца B на ту же ось.
- Алгебраическая проекция вектора AB на ось (вектор) называется длина вектора A'B' , взятая со знаком+или-, в зависимости от того, имеет ли вектор A'B' то же направление, что и ось (вектор).
Виды проекций по системе координат
- проекции на плоскости (система координат OX,OY). Пример: a (2;-3), a =2i-3j
- проекции в пространстве (система координат OX,OY, OZ). Пример: a (2;-3;1), a =2i-3j+k
- проекции в N-мерном пространстве
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.AC' = AB' + B'C'
Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:Прab = |b|·cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак. |
| Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак. |
| Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB. |
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор). |
Проекция точки это. Проекция точки.
Проекция геометрического объекта на одну плоскость не дает полного и однозначного представления о самом геометрическом объекте. Рассмотрим проецирование на две взаимно перпендикулярные плоскости (рис. 1.4), одна из которых расположена горизонтально, а другая вертикально.
Несмотря на наглядность, с чертежом, где проекция точки расположена в пространстве (рис. 1.4, ), работать неудобно, т. к. горизонтальная плоскость на нем показана с искажением. Удобнее выполнять различные построения на чертеже, где плоскости проекций расположены в одной плоскости, а именно, плоскости чертежа. Для этого надо горизонтальную плоскость развернуть вокруг оси на 90° и совместить с фронтальной так, чтобы передняя пола горизонтальной плоскости ушла вниз, а задняя – вверх. Этот метод предложил Г. Монж, поэтому чертеж, полученный таким образом (рис. 1.4, ) называется эпюром Монжа или .
О
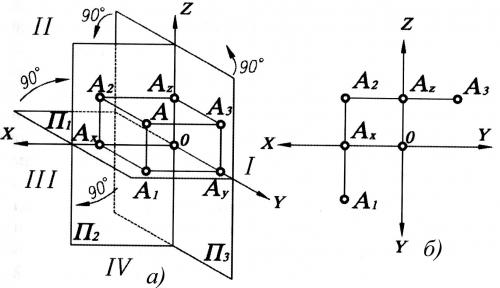
Оси OX , OY , OZ называются осями проекций. Они аналогичны координатным осям декартовой системы координат с той лишь разницей, что ось ОХ имеет положительное направление не вправо, а влево. Теперь, чтобы получить проекции в одной плоскости (плоскости чертежа), необходимо и профильную плоскость проекций развернуть до совмещения с фронтальной. Для этого ее нужно развернуть на 90° вокруг оси OZ , причем переднюю полу плоскости развернем вправо, а заднюю влево. В результате получим трехкартинный комплексный чертеж (эпюр Монжа), показанный на рис 1.5, б. Так как ось OY разворачивается вместе с двумя плоскостями П и П , то на комплексном чертеже ее изображают дважды.
Исходя из рис. 1.5, а , очевидно, что А А = OA = А А . Из этого следует важное правило взаимосвязи проекций: расстояние от горизонтальной проекции точки до оси равно расстоянию от профильной проекции точки до оси . Тогда по двум любым проекциям точки можно построить третью. Горизонтальную и фронтальную проекции точки А связывает вертикальная линия связи, а фронтальную и профильную проекции – горизонтальная.
В связи с тем, что комплексный чертеж представляет собой свернутую в плоскость модель пространства, на нем нельзя изобразить проецируемую точку (за исключением случаев, когда ее положение совпадает с одной из проекций). На комплексном чертеже мы оперируем не самими геометрическими объектами, а их проекциями.
Выше было показано, что две проекции точки определяют ее положение в пространстве. Так как каждая фигура или тело представляет собой совокупность точек, то можно утверждать, что и две ортогональные проекции предмета (при наличии буквенных обозначений) вполне определяют его форму.
Однако в практике для изображения изделий, машин и различных инженерных конструкций возникает необходимость в создании дополнительных проекций. Поступают так с единственной целью — сделать проекционный чертеж более ясным, удобочитаемым.
Модель трех плоскостей проекций показана на рис. 1.6, а . Третья плоскость, перпендикулярная П и П , обозначается буквой П и называется профильной. Проекции точек на эту плоскость будут также именоваться профильными.
Плоскости проекций, попарно пересекаясь, определяют три оси: OX , OY , OZ , которые можно рассматривать как систему прямоугольных декартовых координат в пространстве с началом в точке О. Три плоскости проекций делят пространство на восемь трехгранных углов — это так называемые октанты.
Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте.
Д
ля получения эпюра плоскости Пи вращают, как показано на рис. 1.6, , до совмещения с плоскостью . В результате вращения передняя полуплоскость оказывается совмещенной с нижней полуплоскостью , а задняя полуплоскость — с верхней полуплоскостью . При повороте на 90° вокруг оси передняя полуплоскость совместится с правой полуплоскостью , а задняя полуплоскость — с левой полуплоскостью .Окончательный вид всех совмещенных плоскостей проекций дан на рис. 1.6, . На этом чертеже оси и лежащие в неподвижной плоскости , изображены только один раз, а ось показана дважды. Объясняется это тем, что, вращаясь с плоскостью , ось на эпюре совмещается с осью а вращаясь вместе с плоскостью , эта же ось совмещается с осью .
Горизонтальная Проекция точки. Центральное проецирование
Проецирование (лат. Projicio – бросаю вперёд) – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.
Центральное проецирование заключается в проведении через каждую точку ( А, В, С ,…) изображаемого объекта и определённым образом выбранный центр проецирования ( S ) прямой линии ( SA , SB , >… — проецирующего луча ).
Введём следующие обозначения (Рисунок 1.1):
S – центр проецирования (глаз наблюдателя);
π1 – плоскость проекций;
A, B, C – объекты проецирования – точки;
SA , SB – проецирующие прямые (проецирующие лучи).
Примечание : левой клавишей мыши можно переместитьКРАСНУЮточку в горизонтальной плоскости, при щелчке на точке левой клавишей мыши, изменится направление перемещения и её можно будет переместить по вертикали.
Центральной проекцией точки называется точка пересечения проецирующей прямой, проходящей через центр проецирования и объект проецирования (точку), с плоскостью проекций.
Свойство 1 . Каждой точке пространства соответствует единственная проекция, но каждой точке плоскости проекций соответствует множество точек пространства, лежащих на проецирующей прямой.
Докажем это утверждение.
На рисунке 1.1: точка А 1– центральная проекция точки А на плоскости проекций π1. Но эту же проекцию могут иметь все точки, лежащие на проецирующей прямой. Возьмём на проецирующей прямой SA точку С . Центральная проекция точки С ( С 1) на плоскости проекций π1 совпадает с проекцией точки А ( А 1):
- С ∈ SA ;
- SC ∩ π1= C 1 → C 1 ≡ A 1.
Следует вывод, что по проекции точки нельзя судить однозначно о её положении в пространстве.
Чтобы устранить эту неопределенность, т.е. сделать чертеж обратимым , введём еще одну плоскость проекций (π2) и ещё один центр проецирования ( S 2) (Рисунок 1.2).
Рисунок 1.2 – Иллюстрация 1-го и 2-го свойств
Построим проекции точки А на плоскости проекций π2. Из всех точек пространства только точка А имеет своими проекциями А 1 на плоскость π1 и А 2 на π2 одновременно. Все другие точки лежащие на проецирующих лучах будут иметь хотя бы одну отличную проекцию от проекций точки А (например, точка В ).
Свойство 2 . Проекция прямой есть прямая.
Докажем данное свойство.
Соединим точки А и В между собой (Рисунок 1.2). Получим отрезок АВ , задающий прямую. Треугольник Δ SAB задает плоскость, обозначенную через σ. Известно, что две плоскости пересекаются по прямой: σ∩π1= А 1 В 1, где А 1 В 1 – центральная проекция прямой, заданной отрезком АВ .
Метод центрального проецирования – это модель восприятия изображения глазом, применяется главным образом при выполнении перспективных изображений строительных объектов, интерьеров, а также в кинотехнике и оптике. Метод центрального проецирования не решает основной задачи, стоящей перед инженером – точно отразить форму, размеры предмета, соотношение размеров различных элементов.











