Как узнать, что точка принадлежит прямой. Как определить, лежат ли точки на одной прямой

Как узнать, что точка принадлежит прямой. Как определить, лежат ли точки на одной прямой

Если вам даны две точки, то вы можете смело заявить, что они лежат на одной прямой, так как через любые две точки можно провести прямую. Но как же выяснить, лежат ли все точки на прямой, если точек три, четыре или больше? Доказать принадлежность точек одной прямой можно несколькими способами.

Статьи по теме:

• Как определить, лежат ли точки на одной прямой
• Как найти точку на прямой
• Как провести прямую через две точки

Вам понадобится

• Точки, заданные координатами.

Инструкция

1

Если вам даны точки с координатами (х1, у1, z1), (х2, у2, z2), (х3, у3, z3), найдите уравнение прямой, используя координаты любых двух точек, например, первой и второй. Для этого подставьте соответствующие значения в уравнение прямой: (х-х1)/(х2-х1)=(у-у1)/(у2-у1)=(z-z1)/(z2-z1). Если один из знаменателей равен нулю, просто приравняйте к нулю числитель.

2

Найти уравнение прямой, зная две точки с координатами (х1, у1), (х2, у2), еще проще. Для этого подставьте значения в формулу (х-х1)/(х2-х1)=(у-у1)/(у2-у1).

3

Получив уравнение прямой, проходящей через две точки, подставьте значения координат третьей точки в него вместо переменных х и у. Если равенство получилось верное, значит все три точки лежат на одной прямой. Точно так же можете проверять принадлежность этой прямой других точек.

4

Проверьте принадлежность всех точек прямой, проверив равенство тангенсов углов наклона соединяющих их отрезков. Для этого проверьте, будет ли верным равенство (х2-х1)/(х3-х1)=(у2-у1)/(у3-у1)=(z2-z1)/(z3-z1). Если один из знаменателей равен нулю, то для принадлежности всех точек одной прямой должно выполняться условие х2-х1=х3-х1, у2-у1=у3-у1, z2-z1=z3-z1.

5

Еще один способ проверить принадлежность трех точек прямой – посчитайте площадь треугольника, который они образуют. Если все точки лежат на прямой, то его площадь будет равна нулю. Подставьте значения координат в формулу: S=1/2((х1-х3)(у2-у3)-(х2-х3)(у1-у3)). Если после всех вычислений вы получили ноль - значит, три точки лежат на одной прямой.

6

Чтобы найти решение задачи графическим способом, постройте координатные плоскости и найдите точки по указанным координатам. Затем проведите прямую через две из них и продолжите до третьей точки, посмотрите, пройдет ли она через нее. Учтите, этот способ подходит только для точек, заданных на плоскости с координатами (х, у), если же точка задана в пространстве и имеет координаты (х, у, z), то такой способ неприменим.

Прямая проходит через точки. Уравнение прямой по двум точкам

Получить уравнение прямой по двум точкам бывает необходимо, когда мы решаем задачи, связанные с анализом различных фигур на плоскости. В этом случае бывает полезно знать уравнение прямой, проходящей через две точки. Например, составляя такое уравнение мы уже знаем – как проходит прямая, с какие углом наклона к осям координат и можем рассчитать расположение прямой по отношению к другим прямым или к фигурам.

Составляем уравнение прямой по двум точкам

Итак, пусть нам даны две точкии. Наша прямая проходит через две эти точки, давайте получим уравнение этой прямой. Уравнение пучка прямых, проходящих через точку с координатамиимеет вид:

То есть если прямая проходит через две точкииона – одна из этого пучка прямых, проходящих через точкуи эта прямая имеет определенный коэффициент. Значит, координаты точкидолжны удовлетворять уравнению (1), то есть

.

Находим из (2):

и подставим в уравнение (1):

.

Преобразовывая уравнение (3) получим:

Примечание: если точкиилежат на прямой, которая параллельна осиили оси, то уравнение прямой будет иметь видилисоответственно.

Зная координаты любых двух точек прямой, мы всегда сможем определить угловой коэффициент прямой:

Геометрический вывод уравнения прямой

Действительно, давайте нарисуем прямую в системе координати отметим на прямой две точкии, координаты которых известныии отметим на этой прямой произвольную точку.

Из подобия треугольниковинаходим:

Из рисунка видно, что:

,

Таким образом, получаем уравнение прямой по двум точкам:

Задача

Составим уравнение прямой, проходящей через две точкии.

Как доказать, что точки лежат на одной прямой без координат. Лежат ли 3 точки на прямой. Как определить, лежат ли точки на одной прямой

Очень часто при решения домашней работы возникает вопрос: когда 3 точки лежат на одной прямой, ответ очень прост и он лежит в основе геометрии.

Осуществить проверку того, что три точки лежат на одной прямой можно через составления уравнения, рассматриваемой прямой, которая проходит через две наугад выбранные точки из этих трех. И проверки того, что этому уравнению удовлетворяют координаты оставшейся из этих трех точек.

Есть разные виды уравнения прямой. Воспользуемся одним из простейших способов и рассмотрим его для конкретно заданных точек.

Это сделаем лишь для того, чтобы не решать поставленную задачу в общем виде, а чтобы дать ответ на вопрос лежат ли 3 именно эти точки с этими координатами на одной прямой. Сформулируем задачу: Необходимо проверить лежат ли точки A(-2;1), Б(0;3), В (5;-7) на одной прямой.

Решим поставленную задачу

Как известно, через любые две точки можно провести прямую, причем единственную. Вот и проведем мысленно эту прямую. Допустим, прямую АБ. Значит, решение нашей задачи свелось к тому, что нужно проверить: принадлежит ли точка В прямой АБ. Если окажется, что точка В принадлежит прямой АБ, то все точки из условия будут лежать на одной прямой. Если мы выясним, что точка В не принадлежит прямой АБ, то можно будет утверждать, что точки А, Б и В на одной прямой не лежат. Составим уравнение прямой АБ как уравнение прямой проходящей через две точки:

(х+2)/(0+2)=(y-1)/(3-1)

После преобразования получим:

x-y=-3 - это уравнение прямой АБ

Проверим удовлетворяют ли координаты точки В этому уравнению, для этого достаточно выполнить подстановку координат точки В в место переменных в уравнении прямой АБ. Если получим верное числовое равенство, то точка В - это точка прямой АБ. В противном случае, неверное числовое равенство, будет свидетельствовать о не принадлежности точки В прямой АБ.

Как видим, не получили верное числовое равенство. Значит в этом случае точки А, Б, В не лежат на одной прямой.

Пример, когда 3 точки лежат на одной прямой можно легко подобрать для этой задачи. Всего лишь точка В должна иметь координаты (0;3) или (-7;-4)

Если вам даны две точки , то вы можете отважно заявить, что они лежат на одной прямой , потому что через всякие две точки дозволено провести прямую. Но как же узнать, лежат ли все точки на прямой , если точек три, четыре либо огромнее? Подтвердить принадлежность точек одной прямой дозволено несколькими методами.

Вам понадобится

• Точки, заданные координатами.

Инструкция

1. Если вам даны точки с координатами (х1, у1, z1), (х2, у2, z2), (х3, у3, z3), обнаружьте уравнение прямой , применяя координаты всяких 2-х точек, скажем, первой и 2-й. Для этого подставьте соответствующие значения в уравнение прямой : (х-х1)/(х2-х1)=(у-у1)/(у2-у1)=(z-z1)/(z2-z1). Если один из знаменателей равен нулю, примитивно приравняйте к нулю числитель.

2. Обнаружить уравнение прямой , зная две точки с координатами (х1, у1), (х2, у2), еще проще. Для этого подставьте значения в формулу (х-х1)/(х2-х1)=(у-у1)/(у2-у1).

3. Получив уравнение прямой , проходящей через две точки , подставьте значения координат третьей точки в него взамен переменных х и у. Если равенство получилось правильное, значит все три точки лежат на одной прямой . Верно так же можете проверять принадлежность этой прямой других точек.

4. Проверьте принадлежность всех точек прямой , проверив равенство тангенсов углов наклона соединяющих их отрезков. Для этого проверьте, будет ли правильным равенство (х2-х1)/(х3-х1)=(у2-у1)/(у3-у1)=(z2-z1)/(z3-z1). Если один из знаменателей равен нулю, то для принадлежности всех точек одной прямой должно выполняться условие х2-х1=х3-х1, у2-у1=у3-у1, z2-z1=z3-z1.

5. Еще один метод проверить принадлежность 3 точек прямой – посчитайте площадь треугольника, тот, что они образуют. Если все точки лежат на прямой , то его площадь будет равна нулю. Подставьте значения координат в формулу: S=1/2((х1-х3)(у2-у3)-(х2-х3)(у1-у3)). Если позже всех вычислений вы получили нуль – значит, три точки лежат на одной прямой .

6. Дабы обнаружить решение задачи графическим методом, постройте координатные плоскости и обнаружьте точки по указанным координатам. После этого проведите прямую через две из них и продолжите до третьей точки , посмотрите, пройдет ли она через нее. Учтите, данный метод подходит только для точек, заданных на плоскости с координатами (х, у), если же точка задана в пространстве и имеет координаты (х, у, z), то такой метод неприменим.

Как показать, что точка лежит на прямой. Как определить лежит ли точка на прямой

Урок из серии « Геометрические алгоритмы »

Здравствуйте, дорогой читатель!

Сегодня мы рассмотрим еще одну типовую задачу из серии геометрические алгоритмы. Напишем функцию, которая будет проверять принадлежность произвольной точки отрезку , заданному координатами своего начала и конца.

Для реализации операций сравнения над вещественными данными напишем еще две функции: функцию EqPoint(), которая ,будет проверять, совпадают ли две точки на плоскости и функцию RealMoreEq() , которую будем использовать для проверки отношения «>=» (больше или равно). Причина ввода специальных функций нам уже известна.

Задача. Проверить, принадлежит ли точка отрезку .

Пусть точки— начальная и конечные точки отрезка.— произвольная точка на плоскости.

Вектор с началом в точкеи концом в точкебудет иметь координаты (x2-x1, y2-y1).

Если P(x, y) – произвольная точка, то координаты вектораравны: (x-x1, y – y1).

Точка Р будет принадлежать отрезку если:

1. Векторы виколлинеарны (равно нулю их векторное произведение):
   , т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1) = 0
2. Абсцисса точки P удовлетворяет условию:или. Иначе точка будет находиться на прямой левее или правее отрезка.

Результаты выполнения программы.

Введите координаты точек: x1, y1, x2, y2, x,y
0.5 1 2.5 2.8 1.203 1.633
Да.

Результаты тестирования в программе GeoGebra:

Сегодня мы написали функцию AtOtres() , которая проверяет принадлежность произвольной точки отрезку, заданному своими координатами.

Ввели еще две функции: EqPoint() и RealMoreEq() для реализации операций сравнения над вещественными данными. Первая проверяет, совпадают ли две точки на плоскости, вторая — используется для проверки отношения «>=».

На следующем уроке, на основе ранее написанных процедур, напишем процедуру определения координат точки пересечения двух отрезков.

На этом я с вами прощаюсь. До встречи на следующем уроке.

Ответ

Проверено экспертом

Точка лежит на прямой, если её координаты удовлетворяют уравнению прямой, т.е. при их подстановке вместо неизвестных (х и у) получается верное числовое равенство.

а(-5;3)
-5-4*3+7=0 ?
-5-12+7≠0
-10≠0 => точка А не принадлежит прямой

в(9;4)
9-4*4+7=0 ?
9-16+7=0
0=0 => В лежит на прямой, заданной уравнением х-4у+7=0

Как в canvas определить лежит ли точка на прямой. Уточню — прямая толстая, то есть по сути это наклонный прямоугольник.

Пробовал по формуле взятой из этого вопроса и с небольшой погрешностью.

В случае с наклонными линиями все работает. Но если линия горизонтальная или вертикальная, то вычисление по данной формуле равно Infinity . А если прямых несколько, то соответственно не определить, на которой из них располагается точка

Подскажите пожалуйста алгоритм.

1 ответ 1

Проще всего воспользоваться псевдоскалярным произведением.

Лежит ли точка на прямой онлайн. Точка внутри треугольника

Онлайн калькулятор определяет лежит ли точка внутри треугольника + показывает это наглядно на координатной плоскости .
Под калькулятором вы найдете способ определения принадлежности точки треугольнику.

Известны координаты вершин треугольника и известный координаты точки. Нужно установить принадлежность точки треугольнику.
Существует несколько способов определения. лежит-ли точка внутри треугольника или снаружи:
1. Метод сравнения площадей - по формуле Герона находятся площади 3-х треугольников которые образует точка с каждой стороной треугольника, далее находится площадь самого треугольника и сравнивается с суммой 3ех предыдущих треугольников, если суммы равны то значит точка принадлежит треугольнику.
2. Метод относительности - выбирается ориентация движения по вершинам треугольника, например по часовой стрелке. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Если точка для всех прямых, лежит с правой стороны, то значит точка принадлежит треугольнику, если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.
3. Метод геометрического луча - из точки пускается луч по какой-либо оси в каком-либо направлении. Вычисляется количество пересечений со сторонами, если кол-во нечётное, то значит точка лежит внутри многоугольника.

Если точка лежит на прямой, то можно сказать, что она принадлежит этой прямой. Точка и прямая

Точка и прямая являются основными геометрическими фигурами на плоскости.

Определение точки и прямой в геометрии не вводят, эти понятия рассматриваются на интуитивно-понятийном уровне.

Точки обозначают прописными (заглавными, большими) латинскими буквами: A, B, C, D, …

Прямые обозначают одной строчной (маленькой) латинской буквой, например,

— прямая a.

Прямая состоит из бесконечного множества точек и не имеет ни начала, ни конца. На рисунке изображают только часть прямой, но понимают, что она простирается в пространстве бесконечно далеко, неограниченно продолжаясь в обе стороны.

О точках, которые лежат на прямой, говорят, что они принадлежат этой прямой. Принадлежность отмечают знаком ∈. О точках вне прямой говорят, что они не принадлежат этой прямой. Знак «не принадлежит» — ∉.

Например, точка B принадлежит прямой a (пишут: B∈a),

точка F не принадлежит прямой a, (пишут: F∉a).

Основные свойства принадлежности точек и прямых на плоскости:

Каковы бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и притом только одну.

Прямые также обозначают двумя большими латинскими буквами, по названию точек, которые лежат на прямой.

— прямая AB.

— эту прямую можно назвать MK или MN или NK.

Две прямые могут пересекаться и не пересекаться. Если прямые не пересекаются, они не имеют общих точек. Если прямые пересекаются, они имеют одну общую точку. Знак пересечения — ∩ .

Например, прямые a и b пересекаются в точке O

(пишут: a ∩ b=O).

Прямые c и d также пересекающиеся, хотя на рисунке нет их точки пересечения.

Прямые m и n не имеют общих точек.

Проверить лежит ли точка м на прямой. Как проверить, что точки не лежат на одной прямой

На основании аксиомы, описывающей свойства прямой: какова бы ни была прямая, есть точки, принадлежащие и не принадлежащие ей. Поэтому вполне логично, что не все точки будут лежать на одной прямой линии.

Вам понадобится

• - карандаш;
• - линейка;
• - ручка;
• - тетрадь;
• - калькулятор.

Инструкция

1

Проверить принадлежность точки той либо иной прямой довольно просто. Используйте для этого уравнение прямой. Итак, предположим, что прямая проходит через точки А(x1,y1) и В(x2,y2). Дана точка К(x,y): нужно проверить ее принадлежность прямой. Уравнение линии по двум точкам имеет следующий вид: (x - x1) * (y2 - y1) - (x2 - x1) * (y - y1) = 0.

2

Подставьте значение координат точки К в уравнение. Если (x - x1) * (y2 - y1) - (x2 - x1) * (y - y1) окажется больше нуля, то точка К расположена правее или ниже прямой, проведенной по точкам А и В.

3

В том случае, если (x - x1) * (y2 - y1) - (x2 - x1) * (y - y1) будет меньше нуля, точка К располагается выше или левее линии. Другими словами, только в том случае, если уравнение вида (x - x1) * (y2 - y1) - (x2 - x1) * (y - y1) = 0 справедливо, точки А, В и К будут расположены на одной прямой.

4

В остальных случаях лишь две точки (А и В), которые, по условию задания, лежат на прямой, будут ей принадлежать: через третью точку (точку К) прямая проходить не будет.

5

Рассмотрите второй вариант определения принадлежности точки примой: на этот раз нужно проверить принадлежит ли точка С(x,y) отрезку с концевыми точками В(x1,y1) и А(x2,y2), который является частью прямой z.

6

Точки рассматриваемого отрезка опишите уравнением pOB+(1-p)OА=z, при условии, что 0≤p≤1. ОВ и ОА являются векторами. Если есть такое число p, которое больше или равно 0, но меньше или равно 1, то pOB+(1-p)OА=С, а значит, точка С будет лежать на отрезке АВ. В противном случае, данная точка не будет принадлежать этому отрезку.

7

Распишите равенство pOB+(1-p)OА=С покоординатно: px1+(1-p)x2=x и py1+(1-p)y2=y.

8

Найдите из первого уравнения число р и подставьте его значение во второе равенство. Если равенство будет соответствовать условиям 0≤p≤1, то точка С принадлежит отрезку АВ.

9

Постройте точки по заданным координатам и проведите через них прямую. Это позволит увидеть точки, лежащие на одной прямой, и те точки, что не принадлежат ей.

Обратите внимание

Убедитесь в правильности расчетов!

Полезный совет

Чтобы найти k - угловой коэффициент прямой, нужно (y2 - y1)/(x2 - x1).

Точка принадлежит прямой обозначение. Точки, Прямые и Отрезки — Определения и Свойства

Обновлено

Вспомним определения точки и прямой:

Точка — это фигура в геометрии, не имеющая никаких
измеримых характеристик, кроме координат.

Прямая — это фигура в геометрии, которая не
имеет ни начала, ни конца.

Для изображения прямых на чертеже используют линейку, но
при этом можно изобразить только часть прямой, а вся прямая бесконечна.
Принято обозначать прямые малыми латинскими буквами, а точки —
большими латинскими буквами.

На рисунке 1 изображены прямая c и точки A , B , D , E . Точки А и B
лежат на прямой c , а точки D и E не лежат. Прямая с проходит через
точки A и B, но не проходит через точки С и D . Также заметим, что через
точки A и В нельзя провести другую прямую, не совпадающую с прямой c .

Через любые две точки можно провести прямую,
и притом только одну.

Если две прямые имеют общую точку, то можно сказать,
что они пересекаются. На рисунке 2 прямые a и b
пересекаются в общей точке C , а прямые e и f не
пересекаются, так как не имеют общей точки. Две прямые
не могут иметь двух и более общих точек, так как через две
и более точек проходит только одна прямая.

Две прямые имеют только одну общую точку,
либо не имеют общих точек.

Прямую, на которой отмечены две точки, иногда обозначают двумя
буквами. Для обозначения того, лежит ли точка на прямой или нет,
используют математический символ ∈ или ∉ . Пример использования
математического символа ∈ или ∉ на рисунке 3 .

Часть прямой ограниченная двумя точками называется отрезком . Точки,
ограничивающие отрезок, называются концами отрезка . Отрезок имеет
начало и конец. Пример отрезка на рисунке 4.

Как доказать, что точка лежит на прямой. Теорема Чевы

Определение. Чевианой треугольника называется отрезок, соединяющий вершину треугольника с произвольной точкой противолежащей стороны или ее продолжения (см. рисунок 1).

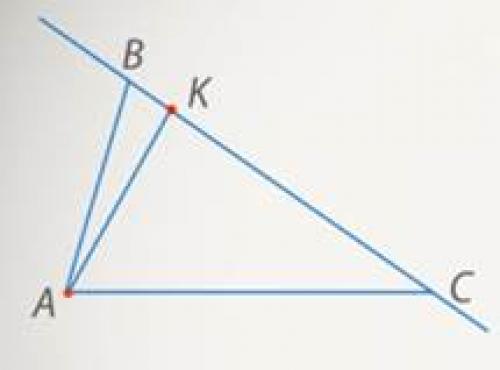
Рис. 1. Пример чевианы

Соответственно, биссектриса, высота и медиана – чевианы. Как вы помните, и высоты, и медианы, и биссектрисы в треугольнике пересекаются в одной точке (см. рисунок 2).

Рис. 2. Пересечение некоторых чевиан в одной точке

Теорема Чевы. Чевианы,ипересекаются в одной точке тогда и только тогда, когда(см. рисунок 3).

Рис. 3. Пересечение чевиан

Доказательство

1) Докажем сперва, что если чевианы пересекаются в одной точке, то выполняется соотношение.

Пусть чевианы,итреугольникапересекаются в точке(см. рисунок 3).

Рассмотрим треугольникии(см. рисунок 4).

Рис. 4. Треугольникии

Поскольку основанияилежат на одной прямой, то у этих треугольников общая высота, опущенная из точки(из точкиможно опустить только одну высоту на прямую– см. рисунок 5). Отсюда следует, что площади этих треугольников относятся так же, как их основания:

Рис. 5. Высоты рассматриваемых треугольников совпадают

Аналогично можно выписать еще два соотношения:;.

Перемножая эти три равенства получаем:

Рассмотрим левую часть данного равенства. Запишем её иначе. Треугольникииимеют равные углы (вертикальные, при вершине– см. рисунок 6). Значит, их площади относятся как произведения длин сторон, заключающих этот угол.

Рис. 6. Треугольники с равными углами

То есть:. Аналогично можно выписать еще два соотношения:;. Перемножая эти равенства, получаем:.

Имеем:

Что и требовалось доказать.

2) Теперь докажем, что если соотношениевыполнено, то три чевианы пересекаются в одной точке.

Воспользуемся методом от противного. Пусть это не так и– точка пересеченияи, ане проходит через эту точку. Проведем чевианучерез точкии(см. рисунок 7).

Рис. 7. Иллюстрация к доказательству теоремы Чевы

Тогда для чевиан,ивыполняется условие теоремы Чевы, которое мы уже доказали:.

Но с другой стороны известно, что

Приравняв левые части двух равенств, имеем:а значит две точки разбили один и тот же отрезок в одном и том же отношении. Единственный случай, когда это возможно, еслиисовпадают. То есть исходное предположение неверно, и значит, все чевианы проходят через одну точку, ч.т.д.