Принадлежность точки прямой линии

Принадлежность точки прямой линии

Если точка принадлежит прямой, то ее проекции принадлежат одноименным проекциям этой прямой. Обратное заключение справедливо для всех прямых кроме профильных уровня.

Рис. 30. Эпюр прямой

Проекции точки D лежат на одноименных проекциях прямой АВ , следовательно, точка D принадлежит прямой АВ (рис. 30). Фронтальная проекция точки С принадлежит фронтальной проекции прямой АВ , а горизонтальная проекция С₁ не лежит на горизонтальной проекции прямой АВ , следовательно, точка С не принадлежит прямой АВ .

На рис. 31 изображена профильная прямая CD. Точка К расположена таким образом, что ее горизонтальная проекция К₁ принадлежит горизонтальной проекции прямой C₁D₁, а фронтальная проекция К₂ принадлежит фронтальной проекции прямой. Тем не менее, чтобы сделать вывод о принадлежности точки К прямой CD, необходимо построить их третьи проекции – профильные. По чертежу видно, что профильная проекция точки К₃ не лежит на профильной проекции прямой, следовательно, и сама точка не принадлежит прямой. Для всех других прямых, кроме профильной уровня, достаточно проверить принадлежность двух проекций точки одноименным проекциям прямой.

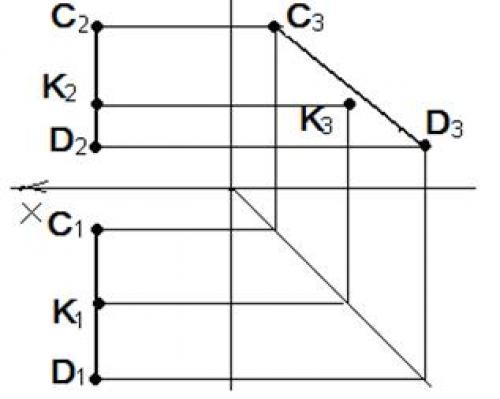
Рис. 31. Профильная прямая

Взаимное положение прямых

2) быть параллельными (лежать в одной плоскости и не иметь общей точки);

3) скрещиваться (лежать в разных плоскостях и не иметь общей точки).

Если прямые параллельны, то одноименные проекции двух параллельных прямых параллельны между собой.

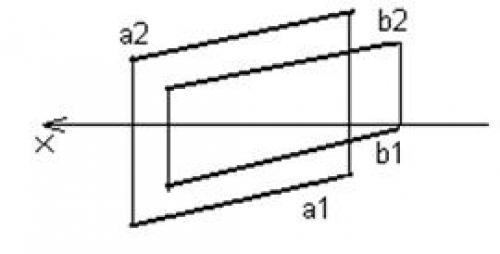
Рис. 32. Эпюр параллельных прямых а и b

Если прямые пересекаются, то их одноименные проекции пересекаются между собой, а проекции точки пересечения лежат на одной линии связи.

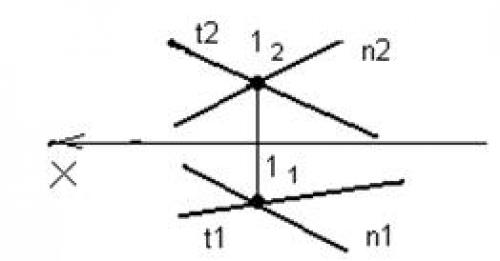
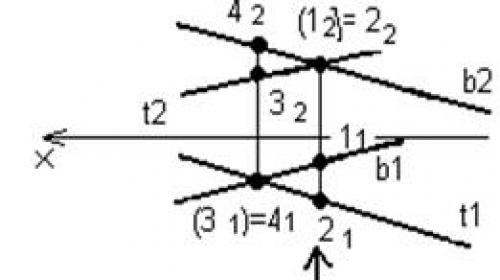
Скрещивающиеся прямые – прямые, которые не пересекаются и не параллельны между собой. На эпюре скрещивающиеся прямые будут напоминать пересекающиеся с той лишь разницей, что точки пересечения фронтальных и горизонтальных проекций не будут лежать на одной линии связи (перпендикуляре к оси ОХ ).

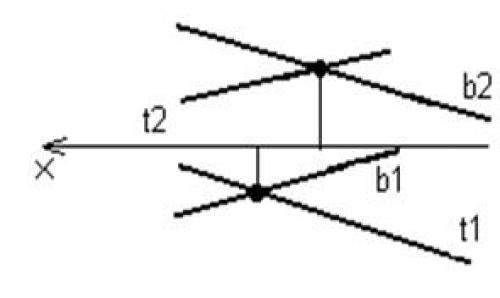
Рис. 34. Скрещивающиеся прямые

Точки, лежащие на одном проецирующем луче, называются конкурирующими.

Плоскости

Плоскость в пространстве определяется:

1) тремя точками, не лежащими на одной прямой;

2) прямой и точкой не принадлежащей ей;

3) двумя параллельными прямыми;

4) двумя пересекающимися прямыми;

5) отсеком плоской фигуры – треугольником, четырехугольником и т. д.

Рис. 36. Задание плоскости тремя точками

Рис. 37. Задание плоскости треугольником

В начертательной геометрии пользуются еще одним способом задания плоскостей – следами.

Следом плоскости называют линию пересечения плоскости с плоскостью проекций.

Плоскость Q пересекается с плоскостями проекций по прямым, называемым следами плоскости: Q₁ – горизонтальный след плоскости, Q₂ – фронтальный, Q₃ – профильный след плоскости. Q_x, Q, Q – точки схода следов на осях проекций.

Рис. 38. Изображение плоскости

Рис. 39. Эпюр плоскости

Часто плоскость на эпюре изображается двумя следами ( Q₁, Q₂ ), которые как две пересекающиеся прямые вполне определяют плоскость. Фронтальный след плоскости расположен во фронтальной плоскости проекций, поэтому его горизонтальная проекция лежит на оси ОХ . Горизонтальный след плоскости расположен в горизонтальной плоскости проекций, его фронтальная проекция лежит на оси .

Плоскость, не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения. Плоскость общего положения пересекается со всеми плоскостями проекций, т. к. не параллельна ни одной из них.

Принадлежность точки плоскости формула. Как составить уравнение плоскости?

Конструировать уравнение плоскости будем с помощью векторов и точек. Их должно быть как можно меньше , но достаточно , чтобы однозначно определить плоскость. Одним словом, красивая математическая лаконичность. Математика – царица наук, не стерва, но строгА. А уж насколько доступна, во многом зависит от вашего к ней отношения =)

Казалось бы, плоскость можно определить с помощью двухнеколлинеарныхвекторов. Но векторы свободны и бродят по всему пространству, поэтому ещё нужна фиксированная точка.

Как составить уравнение плоскости по точке и двум неколлинеарным векторам?

Рассмотрим точку и дванеколлинеарныхвектора. Уравнение плоскости , которая проходит через точку параллельно векторам, выражается формулой :

! Примечание : под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости. Для наглядности я буду откладывать векторы прямо в плоскости.

Принципиально ситуация выглядит так: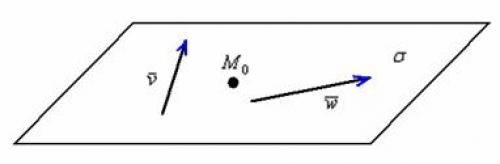
Обратите внимание, что точка и дваколлинеарныхвектора не определят плоскость однозначно (векторы будут свободно «вертеться» вокруг точки и зададут бесконечно много плоскостей).

Пример 1

Составить уравнение плоскости по точке и векторам.

Решение : Составим уравнение плоскости по точке и двум неколлинеарным векторам:

Определитель удобнее всего раскрыть по первому столбцу:

Раскрываем определители второго порядка:

На первом месте у нас находится знак «минус». Хорошим тоном считается убрать наглеца, в этих целях меняем знак у каждого слагаемого. Проводим дальнейшие упрощения и получаем уравнение плоскости:

Сократить здесь ничего нельзя, поэтому:

Ответ :

…числа, конечно, страшноваты получились для первого примера =) …но переделывать, пожалуй, не буду, на практике большие числа – вещь распространённая.

Как проверить задание? Для проверки пока не хватает информации, но я обязательно выполню её чуть позже.

Пример 2

Составить уравнение плоскости по точке и двум неколлинеарным векторам.

Это пример для самостоятельного решения, полное решение и ответ в конце урока.

Иногда может потребоваться решить обратную задачу – по известному уравнению плоскости найти параллельные ей векторы. Кстати, сколько параллельных векторов существует у плоскости? Бесконечно много. Однако нельзя объять необъятное, поэтому «вытащим» из уравнения плоскости три таких вектора:

Пусть плоскость задана общим уравнением. Тогда векторы будут параллельны данной плоскости (а, значит, компланарны ), и любые два из них – линейно независимы. Так, в Примере № 1 мы составили уравнение плоскости. Построенной плоскости будут параллельны следующие векторы:. Если честно, не припомню, чтобы приходилось этим пользоваться, тем не менее, справка не лишняя.

Итак, «конструкция» из двух  неколлинеарных векторов и точки однозначно определяет плоскость. Но существует более очевидный способ, о котором упоминалось выше, и он громким стуком в дверь уже давно просится на урок. Три точки. Дёшево и сердито.

Как составить уравнение плоскости по трём точкам?

Любые ли три точки пространства задают плоскость? Нет. Во-первых, точки должны быть различными. А во-вторых, они не должны лежать на одной прямой (сразу все три).

Взаимное расположение точек в пространстве. Взаимное расположение точки, прямых и плоскостей с примерами

Взаимное расположение точки и прямой:

Возможны два варианта расположения точки относительно прямой:

• - точка принадлежит прямой (рис. 3.1 а), тогда ее проекции на КЧ лежат на одноименных проекциях прямой.
• - точка не принадлежит прямой (рис. 3.1 б), если хотя бы одна из проекций точки не принадлежит проекции прямой

Взаимное расположение прямых

Прямые в пространстве могут занимать друг к другу одно из трех положений:

• - быть параллельными;
• - пересекаться;
• - скрещиваться.

Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.

Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.

У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А . Причем фронтальная и горизонтальная проекции этой точки должны находиться на одной линии связи.

Рис. 3.3

Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.

Рис. 3.4

Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.

На рис. 3.4 точка С принадлежит прямой b , а точка D на прямой   а . Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций.

Плоскость. Способы ее задания, положение относительно плоскостей проекций

Положение плоскости в пространстве может быть однозначно определено:

• - тремя точками, не лежащими на одной прямой;
• - прямой и точкой, не лежащей на этой прямой;
• - двумя параллельными прямыми;
• - двумя пересекающимися прямыми;
• - плоской фигурой;
• - следом плоскости.

След плоскости – это линия пересечения заданной плоскости с одной из плоскостей проекций.

Соответственно различают горизонтальный, фронтальный и профильный следы плоскости.

Плоскостью общего положения называется плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций.

Плоскостями частного положения относительно плоскостей проекций называются плоскости параллельные или перпендикулярные им.

Плоскость перпендикулярная одной из плоскостей проекций называется проецирующей плоскостью.

Существует три вида проецирующих плоскостей: горизонтально- проецирующая, фронтально-проецирующая и профильно-проецирующая плоскости. Такие плоскости вырождаются в прямую линию (след плоскости) на ту плоскость проекций, к которой они перпендикулярны.

1. Горизонтально-проецирующая плоскость  - плоскость перпендикулярная горизонтальной плоскости проекций.

2. Фронтально-проецирующая плоскость – плоскость перпендикулярная фронтальной плоскости проекций.

3. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня.

Существует три вида плоскостей уровня: горизонтальная, фронтальная и профильная плоскости уровня.

1. Горизонтальная плоскость – плоскость, параллельная горизонтальной плоскости проекций.

2. Фронтальная плоскость  - плоскость, параллельная фронтальной плоскости проекций.

Принадлежность точки прямой онлайн. Уравнение прямой проходящей через две точки

Виджет

Ссылка на расчет

Сообщить об ошибке

Сохранить расчет

Печатать

Получить уравнение прямой, проходящей через две точки помогут созданные нами. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая - это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

• каноническое уравнение,
• параметрическое уравнение,
• общее уравнение прямой,
• уравнение прямой с угловым коэффициентом,
• уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.

Каноническое уравнение прямой на плоскости

{\dfrac{x-x_a}{x_b-x_a} = \dfrac{y-y_a}{y_b-y_a}}

x_a и y_a - координаты первой точки A,

x_b и y_b - координаты второй точки B

Параметрическое уравнение прямой на плоскости

{\begin{cases} x=l \cdot t + x_a \\ y=m \cdot t + y_a \end{cases}}

x_a , y_a - координаты точки, лежащей на прямой,

{l;m} - координаты направляющего вектора прямой,

t - произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Каноническое уравнение прямой в пространстве

{\dfrac{x-x_a}{x_b-x_a} = \dfrac{y-y_a}{y_b-y_a} = \dfrac{z-z_a}{z_b-z_a}}

x_a , y_a и z_a - координаты первой точки A,

x_b , y_b и z_b - координаты второй точки B

Параметрическое уравнение прямой в пространстве

{ \begin{cases} x=l \cdot t + x_a \\ y=m \cdot t + y_a \\ z=n \cdot t + z_a \end{cases} }

x_a , y_a и z_a - координаты точки, лежащей на прямой,

{l;m;n} - координаты направляющего вектора прямой,

t - произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.

Пример нахождения уравнения прямой, проходящей через две точки

Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).

Каноническое уравнение прямой

Каноническое уравнение прямой, проходящей через две точки имеет вид {\dfrac{x-x_a}{x_b-x_a} = \dfrac{y-y_a}{y_b-y_a}}

Подставим в формулу координаты точек A и B: {\dfrac{x-1}{3-1} = \dfrac{y-2}{8-2}}

Получаем каноническое уравнение прямой: {\dfrac{x-1}{2} = \dfrac{y-2}{4}}

Уравнение прямой с угловым коэффициентом

Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}

Параметрическое уравнение прямой

Параметрическое уравнение прямой имеет вид:

{ \begin{cases} x=l \cdot t + x_a \\ y=m \cdot t + y_a \end{cases} }

где {x_a, y_b} - координаты точки, лежащей на прямой, {\{l;m\}} - координаты направляющего вектора прямой, t - произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)} .

Найдем координаты направляющего вектора:

\overline{AB} = \{x_b - x_a; y_b - y_a\} = \{3-1; 8-2\} = \{2; 6\}

Получаем параметрическое уравнение:

\begin{cases} x=2 t + 1 \\ y=6 t + 2 \end{cases}

Используем калькулятор дляполученного ответа.

Принадлежность точки прямой формула. Как определить, лежат ли точки на одной прямой

Если вам даны две точки, то вы можете смело заявить, что они лежат на одной прямой, так как через любые две точки можно провести прямую. Но как же выяснить, лежат ли все точки на прямой, если точек три, четыре или больше? Доказать принадлежность точек одной прямой можно несколькими способами.

Статьи по теме:

• Как определить, лежат ли точки на одной прямой
• Как найти точку на прямой
• Как провести прямую через две точки

Вам понадобится

• Точки, заданные координатами.

Инструкция

1

Если вам даны точки с координатами (х1, у1, z1), (х2, у2, z2), (х3, у3, z3), найдите уравнение прямой, используя координаты любых двух точек, например, первой и второй. Для этого подставьте соответствующие значения в уравнение прямой: (х-х1)/(х2-х1)=(у-у1)/(у2-у1)=(z-z1)/(z2-z1). Если один из знаменателей равен нулю, просто приравняйте к нулю числитель.

2

Найти уравнение прямой, зная две точки с координатами (х1, у1), (х2, у2), еще проще. Для этого подставьте значения в формулу (х-х1)/(х2-х1)=(у-у1)/(у2-у1).

3

Получив уравнение прямой, проходящей через две точки, подставьте значения координат третьей точки в него вместо переменных х и у. Если равенство получилось верное, значит все три точки лежат на одной прямой. Точно так же можете проверять принадлежность этой прямой других точек.

4

Проверьте принадлежность всех точек прямой, проверив равенство тангенсов углов наклона соединяющих их отрезков. Для этого проверьте, будет ли верным равенство (х2-х1)/(х3-х1)=(у2-у1)/(у3-у1)=(z2-z1)/(z3-z1). Если один из знаменателей равен нулю, то для принадлежности всех точек одной прямой должно выполняться условие х2-х1=х3-х1, у2-у1=у3-у1, z2-z1=z3-z1.

5

Еще один способ проверить принадлежность трех точек прямой – посчитайте площадь треугольника, который они образуют. Если все точки лежат на прямой, то его площадь будет равна нулю. Подставьте значения координат в формулу: S=1/2((х1-х3)(у2-у3)-(х2-х3)(у1-у3)). Если после всех вычислений вы получили ноль - значит, три точки лежат на одной прямой.

6

Чтобы найти решение задачи графическим способом, постройте координатные плоскости и найдите точки по указанным координатам. Затем проведите прямую через две из них и продолжите до третьей точки, посмотрите, пройдет ли она через нее. Учтите, этот способ подходит только для точек, заданных на плоскости с координатами (х, у), если же точка задана в пространстве и имеет координаты (х, у, z), то такой способ неприменим.

Условие принадлежности точки прямой. Вопро. Взаимное положение прямой и плоскости.

Как доказать, что точка принадлежит прямой. Геометрия 7 класс. Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Запомните!

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

В тексте точку обозначают символом « (·)» . Принадлежность и непринадлежность точки прямой обозначают символами « ∈ » и « ∉ ». Знак принадлежности можно запомнить как зеркальное отображение буквы « Э » или как знак евро « € » .

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

• (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a );
• (·)G ∈ a — точка G принадлежит прямой a ;
• (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a );
• (·)H ∉ a — точка H не принадлежит прямой a .

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

На рисунке изображены:
• Прямая a
• Прямая f
• Прямая CH
• Прямая DK

Точки D, E и F — лежат на одной прямой, поэтому: прямая DE , прямая EF и прямая DF — это три разных имени одной и той же прямой.

Разбор примера

Проведите прямую, обозначьте её буквой a и отметьте точки A и B , лежащие на этой прямой, и точки P, Q и R , не лежащие на ней. Опишите взаимное расположение точек A, B, P, Q, R и прямой a , используя символы ∈ и ∉ .

Решение задачи

Проведём прямую.

Обозначим её буквой a .

Опишем взаимное расположение точек и прямой.

• (·)A ∈ a
• (·)B ∈ a
• (·)P ∉ a
• (·)Q ∉ a
• (·)R ∉ a

Задача решена.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).