Конкурирующие точки и определение их видимости. Лекция 5

Конкурирующие точки и определение их видимости. Лекция 5

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ

Две плоскости могут быть:

параллельными ;

пересекающимися .

Если два следа одной плоскости параллельны одноименным следам другой плоскости, то такие плоскости взаимно параллельны (рис. 46).

Если, хотя бы одна пара одноименных следов двух плоскостей пересекается, то эти плоскости пересекаются (рис. 47).

Когда плоскости заданы не следами, а иным способом, то две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, например (рис. 48): АВ  К L и ВС  КТ .

ПЕРЕСЕКАЮЩИЕСЯ ПЛОСКОСТИ

Линией пересечения двух плоскостей является прямая, все точки которой являются общими для обеих плоскостей. Таким образом, в общем случае для нахождения линии пересечения необходимо найти хотя бы две точки, общих для обеих плоскостей. Такими точками могут быть, например, точки пересечения одноименных следов плоскостей  и  – точки M и N (рис. 49, а). Через них и пройдет линия пересечения. Линия пересечения плоскостей видима только в 1-м октанте (значения координат х,у и z положительные).

На эпюре (рис. 49, б) проекции линии пересечения пройдут через точки пересечения одноименных следов плоскостей  и . В пересечении горизонтальных следов находим проекцию общей точки М  (фронтальная проекция этой точки М  лежит на оси x ), а в пересечении фронтальных следов - N  (горизонтальная проекция N  также лежит на оси x ). Соединив одноименные проекции М и N , получим две проекции линии пересечения на эпюре.

Метод конкурирующих точек пример. Метод конкурирующих точек треугольников

Определение видимости

Определение видимости геометрических фигур на плоскости проекций выполняют с использованием конкурирующих точек.

Определение видимости рассмотрим на примерах: - имеется готовый эпюр пересечения прямой с плоскостью заданной треугольником ABC

Конкурирующие точки находим в пересечении проекций прямой с проекциями треугольника ABC - это точки 1 и 2 их проекции 1` и 2` на плоскость H совпадают. Строим проекции этих точек на плоскости V из условия, что точка 1 принадлежит прямой n, а точка 2 принадлежит стороне треугольника BC. Сравниваем удаление конкурирующих точек 1 и 2 от горизонтальной плоскости проекций - точка 2 является более удаленной. Из проведенного сравнения делаем вывод о видимости заданных геометрических фигур: точка 2 видима и видима плоскость, а точка 1 невидима и ее участок прямой невидим.

- имеется готовый эпюр пересечения прямой с плоскостью заданной следами

Конкурирующие точки находим в пересечении проекций прямой с проекциями плоскости α - для этого проводим в плоскости произвольную прямую f, чтобы имело место пересечение фронтальных проекций заданной прямой n и прямой f. Это точки 1 и 2 их проекции 1" и 2" на плоскость V совпадают. Строим проекции этих точек на плоскости H из условия, что точка 1 принадлежит прямой n, а точка 2 принадлежит фронтали f плоскости α. Сравниваем удаление конкурирующих точек 1 и 2 от фронтальной плоскости проекций - точка 2 является более удаленной. Из проведенного сравнения делаем вывод о видимости заданных геометрических фигур: точка 2 видима и видима плоскость α, а точка 1 невидима и ее участок прямой невидим.

Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.

1. Строим проекции треугольника АВС.

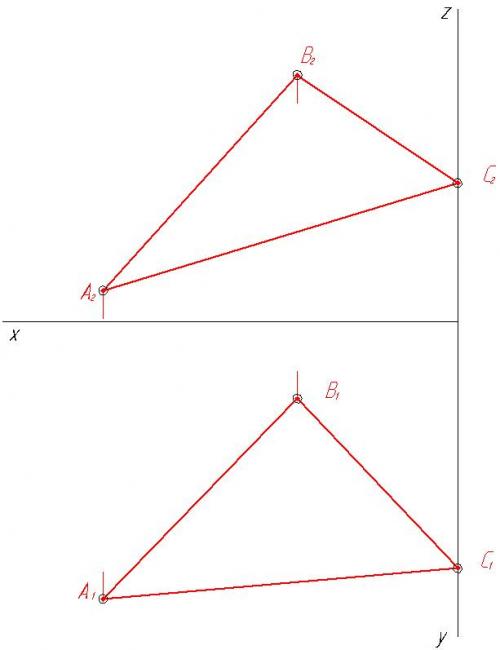
2. Строим проекции треугольника EDK.

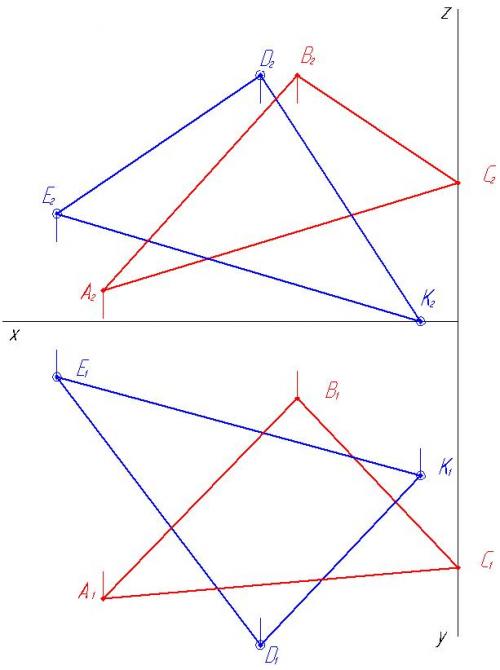
3. Находим точку пересечения стороны АС с треугольником EDK

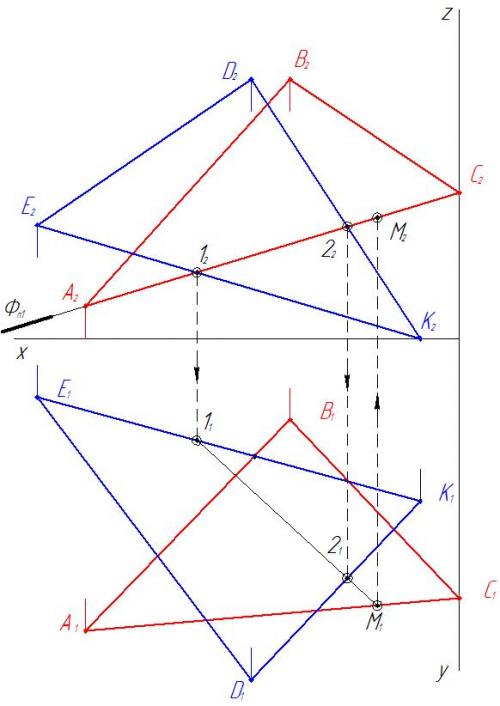
4. Находим точку пересечения стороны А B с треугольником EDK и строим линию пересечения MN

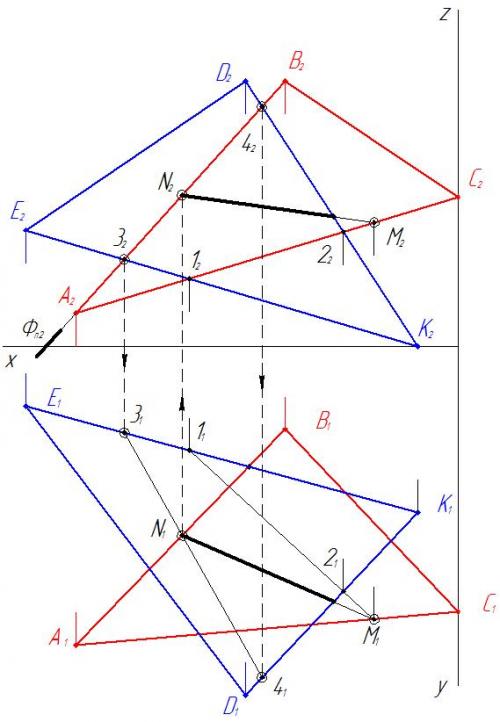
5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.

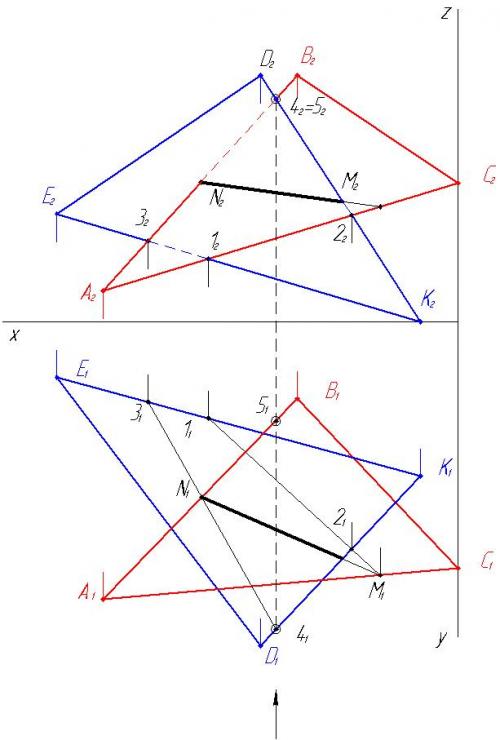
6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.

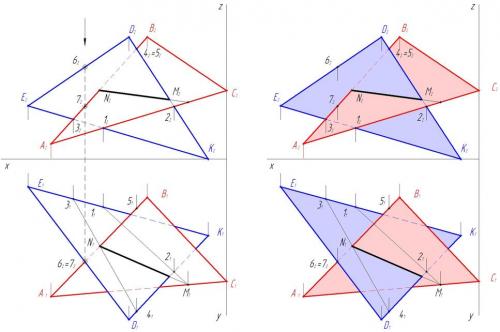
7. В треугольнике ABC проводим горизонталь CL и плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.

Строим фронтальную проекцию треугольника ABC . Треугольник должен проецироваться в прямую линию.

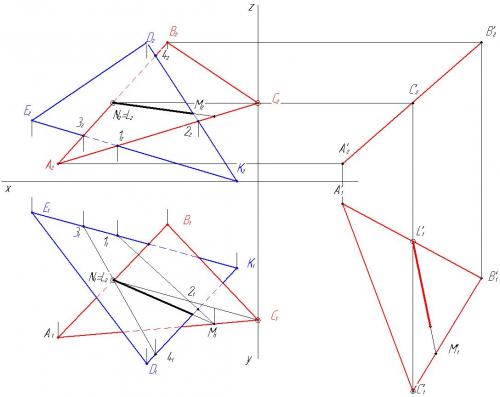
8. Определяем действительную величину треугольника ABC и строим на нем линию пересечения MN.

Метод конкурирующих точек треугольников

Пошаговое руководство решения задачи №1 — «Нахождение линии пересечения двух плоскостей и определение натуральной величины»

В задаче необходимо найти линию пересечения двух плоскостей и определить натуральную величину одной из них методом плоскопараллельного перемещения.

Горизонтально конкурирующие точки. Определение видимости в начертательной геометрии с примерами

Определение видимости:

Точки, расположенные на одной проецирующей прямой, называются конкурирующими.

Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).

Рис. 7.1. Конкурирующие точки: а - относительно горизонтальной плоскости проекций;б - относительно фронтальной плоскости проекций

Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D - невидима).

Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).

Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже: а - относительно горизонтальной плоскости проекций;б - относительно фронтальной плоскости проекций

Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П₁, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П₁, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П₁

Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П₂.

Конкурирующие точки видимость. Конкурирующие точки и определение их видимости

Точки, у которых одна из проекций совпадает (две одинаковые координаты), называются конкурирующими. Плоскость проекций, на которой проекции совпадают, дает название этим точкам ( горизонтально , вертикально и профильно конкурирующие точки) (рис. 3.15, 3.16).

Видимость точек определяем по направлению проецирования (взгляда, направленного в сторону, противоположную положительному отсчету координатных осей, на рис. 3.15, 3.16 - стрелка):

• • для горизонтально конкурирующих точек направление проецирования - сверху вниз на фронтальной и профильной плоскостях проекций;
• • для фронтально конкурирующих точек - снизу вверх на горизонтальной плоскости проекций, справа налево - на профильной плоскости проекций;
• • для профильно конкурирующих - слева направо на горизонтальной и фронтальной плоскостях проекций.

Рис. 3.15

При символьном обозначении видимости сначала указывается проекция видимой точки, а затем в круглых скобках - невидимой. Например, А(В) - горизонтально конкурирующие точки, из которых точкам видна. Для чертежа на рис. 3.16:

Z)₂(C₂) - фронтально конкурирующие;

Рис. 3.16

Умение различать конкурирующие точки и определять их видимость очень важно при решении позиционных задач по определению положения геометрических объектов друг относительно друга. Выбираются конкурирующие точки, принадлежащие различным геометрическим объектам, затем определяется видимость проекций точек, на основании чего делаются выводы о видимости проекций собственно геометрических объектов.

Пример 5

Задание: показать на комплексном чертеже точки А (30, 9, 10), В и С (19, -10, 18). Учесть, что точка В фронтально конкурирует с точкой А и не видна. Причем последняя левее точки С на 11 мм, ниже на 8 мм и ближе на 19 мм. Расстояние между точками Ап В равно 9 мм.

Решение. Для того чтобы начать построение, необходимо определить габариты чертежа - высоту и ширину. Для размера высоты необходимо учесть координаты Z и Y (см. рис. 3.7, 3.8). Максимальная аппликата будет у точки С - Z_c= 18 мм. Учитывая максимальную ординату у точки А - Y_a= 9 мм и то, что ордината точки В меньше, так как она располагается дальше, чем точка А , получим минимальный габаритный размер чертежа по высоте: Z_c + Y_A= 27 мм. Допустим, что высота листа больше, чем полученный минимальный размер. Тогда построение можно начинать либо с фронтальной проекции точки С (наивысшая точка), либо с горизонтальной проекции точки А. Учитывая, что точка А самая левая точка, приходим к выводу, что построение удобнее начинать именно с этой точки, поскольку на чертеже она будет самая левая и нижняя.

На рис. 3.17 начало координат для каждой плоскости проекций не показано, но следует учесть, что здесь начала координат для каждой плоскости проекций не совпадают, т. е. фронтальная плоскость проекций смещена по вертикали, а профильная - по горизонтали.

Рис. 3.17

Построение горизонтальных проекций точек выполним в определенной последовательности. Обозначим положение проекции точки А - А (рис. 3.17). Показываем вертикальную линию связи. Так как точки А и В фронтально конкурирующие, то они имеют одинаковые координаты Z и X, а значит, располагаются на одной вертикальной линии связи. Учитывая, что точки имеют одинаковую высоту (одинаковая аппликата), расстояние между этим точками будет равно разности ординат - А7= 9 мм. Выше на 9 мм проекции точки А показываем проекцию точки В - В. Проекция точки С выше проекции точки А на AY= Y_a - Y_c= 9 - (-10) = 19 мм и правее на АХ=Х_а-Х_с= 30 - 19 = = 11 мм, что и показываем на чертеже.

При построении фронтальных проекций точек будем исходить из того, что на фронтальной плоскости проекций самой низшей точкой будет точка А, и построение начинаем именно с этой точки. На вертикальной линии связи данной точки произвольно, учитывая габариты по высоте и размер поля чертежа, показываем положение проекции точек Aw В (фронтально конкурирующие точки - проекции совпали). На вертикальной линии связи точки С выше проекции точки А₂ на расстояние A Z = Zc — Z_A= 18-10 = 8 мм показываем фронтальную проекцию точки С - С₂.

Для построения профильных проекций точек проводим горизонтальные линии связи. Начинаем построение с самой дальней точки, так как на профильной проекции самая левая проекция будет у той точки, которая находится дальше всех. Для нашей задачи (определяем по горизонтальной проекции) это будет точка С. На ее горизонтальной линии связи показываем проекцию точки С - Сз. При этом необходимо учесть, что чертеж будет правее - на расстоянии от самой ближней до самой дальней точки чертежа. В нашем случае - А 7 = = Y_a - Yc = 19 мм. На горизонтальной линии связи точек Aw В правее профильной проекции точки С откладываем это расстояние и показываем проекцию точки А - А₃. На этой же линии связи левее проекции точки А з (так как точка А ближе точки Q откладываем 9 мм и отмечаем проекцию точки В - В₃.

Следует отметить, что при решении задачи система координат не показывалась, поскольку в этом нет необходимости.

Из двух конкурирующих точек на комплексном чертеже видна проекция той, которая. Взаимное положение двух точек. Условия видимости на чер­теже

Рассмотрим чертеж модели, изображенной на рис. 3.6. Проекции некоторых точек совпадают, так как они расположены на одной проецирующей прямой. Например, на горизонтальной плоскости совпали проекции а и b вершин А и В - они лежат на одной горизонтально - проецирующей прямой. На фронтальной плоскости совпали проекции с ' и d ' вершин С и D - они лежат на одной фронтально-проецирующей прямой.

Точки, лежащие на одной проецирующей прямой, называют конкурирующими . А и В - горизонтально-конкурирующие точки, а С и D - фронтально-конкурирующие точки и т.д.

Ясно, что если две точки лежат на одной проецирующей прямой, то одна из них закрывает другую. Как определить, какая из них будет видимая и какая невидимая?

Из двух горизонтально- конкурирующих точек на горизонтальной плоскости видима та, которая расположена в пространстве выше. Анализируя положение фронтальных проекций точек (рис. 3.7), определяем, что точка А имеет большую координату z, чем точка В.

Следовательно, точка А расположена выше точки В и при проецировании на горизонтальную плоскость проекций закроет точку В. Точка А на горизонтальной плоскости видима, точка В - невидима. На фронтальной плоскости они обе видимы.

Из двух фронтально- конкурирующих точек на фронтальной плоскости проекций будет видима та, которая расположена ближе к наблюдателю, стоящему лицом к фронтальной плоскости проекций (рис. 3.8).

Какая из точек ближе к на­блюдателю, можно определить по горизонтальным проекциям. Например, сравнивая горизонтальные проекции точек D и С , заключаем, что на фронтальной плоскости проекций видима точка С, а точка D - невидима, так как

Из двух профильно-конкурирующих точек на профильной плоскости проекций бу­дет видима та точка, которая расположена левее.

Итак, если на чертеже одноименные проекции точек не совпадают или совпадает только одна пара проекций, то такие точки в пространстве не совпадают, а удалены друг от друга на определенное расстояние (рис. 3.7, 3.8).

Метод конкурирующих точек. Построение точки пересечения прямой и плоскости

Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h_0α, f_0α.

Алгоритм

1. Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h_0γ, f_0γ.
2. Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B' = h_0α ∩ h_0γ, A'' = f_0α ∩ f_0γ. Точки A' и B'' лежат на оси x, их положение определяется по линиям связи.
3. Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K' = a' ∩ A'B'. Фронтальная проекция K'' лежит на прямой a''.

Алгоритм решения останется тем же, если пл.  α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими.

Видимость прямой a относительно плоскости α. Метод конкурирующих точек

1. Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A'' и С'' совпадают, но при этом т. A и С удалены от плоскости проекций П₂на разное расстояние.
2. Найдем горизонтальные проекции A' и C'. Как видно на рисунке, точка C' удалена от плоскости П₂на большее расстояние, чем т. A', принадлежащая пл. α. Следовательно, участок прямой а'', расположенный левее точки K'', будет видимым. Участок a'' правее K'' является невидимым. Отмечаем его штриховой линией.
3. Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D' и E' совпадают, но при этом т. D и E удалены от плоскости П₁на разное расстояние.
4. Определим положение фронтальных проекций D'' и E''. Как видно на рисунке, точка D'', находящаяся в пл. α, удалена от плоскости П₁на большее расстояние, чем т. E'', принадлежащая прямой a. Следовательно, участок а', расположенный правее точки K', будет невидимым. Отмечаем его штриховой линией. Участок a' левее K' является видимым.