Системы двух и трех плоскостей проекций. Метод Монжа. Октанты пространства

Системы двух и трех плоскостей проекций. Метод Монжа. Октанты пространства

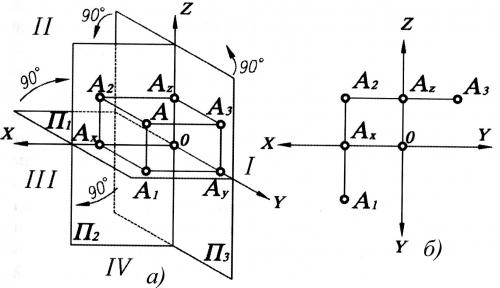
Наиболее важным из них является возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры. При этом при получении ортогонального чертежа, обладающего полной обратимостью, необходимо иметь, как было отмечено ранее, по крайней мере, две связанные между собой ортогональные проекции оригинала. Наиболее удобной для фиксирования положения геометрического образа в пространстве и выявления его формы по ортогональным проекциям является система из трех взаимно перпендикулярных плоскостей проекций. Такой плоскостной макет представлен на рис. 29. При этом различают:

Плоскости проекций пересекаются по трем взаимно перпендикулярным прямым, которые называются осями проекций Оси проекций пересекаются в общей точке трех плоскостей проекций - точке 

В большинстве европейских стран принята система расположения плоскостей проекций, при которой положительными направлениями осей считают: для оси - влево от точкидля оси - в сторону зрителя (вперед) от плоскостидля- вверх от плоскостипротивоположные направления осей считают отрицательными.

Плоскости проекций делят пространство на восемь частей - октантов. Октанты условно принято нумеровать, как показано на рис. 29.

Принято, что наблюдатель всегда находится в первом октанте. Плоскости проекций считаются непрозрачными, поэтому видимы только точки (геометрические фигуры), расположенные в I октанте, а также на полуплоскостях

Пользоваться пространственным макетом для изображения проекций оригинала неудобно ввиду его громоздкости. Поэтому его реконструируют в эпюр Монжа - чертеж, составленный из двух или трех связанных между собой ортогональных проекций геометрической фигуры.

Преобразование пространственного макета в эпюр осуществляется путем совмещения плоскостей ис фронтальной плоскостью проекций

Для совмещения плоскостисповорачиваем на 90° вокруг осив направлении движения часовой стрелки (см. рис. 29).

Для совмещениясповорачиваемвокруг оситакже на угол 90° в направлении, противоположном движению часовой стрелки. При повороте будет перемещаться и оськоторая распадается на две оси (и).

После совмещения плоскостей проекций пространственный макет примет вид, показанный на рис. 30.

Обычно не указывают обозначение полуплоскостей проекций и отрицательное направление осей. Тогда, в окончательном варианте, эпюр принимает вид, показанный на рис. 31.

Проекции точки

Точка - одно из основных базовых понятий геометрии. Для отображения этого простейшего геометрического образа на плоскости целесообразно понимать под точкой физический объект, имеющий линейные размеры. При этом условно за точку принимают шарик с бесконечно малым радиусом. При такой трактовке понятия точки можно говорить о ее проекциях.

Проекции точек, находящихся в пространстве, на плоскостях проекций и на осях проекций.. Проекция точки.

Проекция геометрического объекта на одну плоскость не дает полного и однозначного представления о самом геометрическом объекте. Рассмотрим проецирование на две взаимно перпендикуляр­ные плоскости (рис. 1.4), одна из которых расположена горизонтально, а другая вертикально.

Несмотря на наглядность, с чертежом, где проекция точки расположена в пространстве (рис. 1.4, ), работать неудобно, т. к. горизонтальная плоскость на нем показана с искажением. Удобнее выполнять различные построения на чертеже, где плоскости проекций расположены в одной плоскости, а именно, плоскости чертежа. Для этого надо горизонтальную плоскость раз­вернуть вокруг оси на 90° и совместить с фронтальной так, что­бы передняя пола горизонтальной плоскости ушла вниз, а задняя – вверх. Этот метод предложил Г. Монж, поэтому чертеж, получен­ный таким образом (рис. 1.4, ) называется эпюром Монжа или .

О

бычно двух проекций недостаточно, чтобы составить полное представление о рассматриваемом геометрическом объекте. Поэтому предлагается ввести третью плоскость проекций, ортого­нальную первым двум. (Рис. 1.5, а ) Тогда плоскость П называется горизонтальной плоскостью проекций, П - фронтальной плоскостью проекций (т. к. она расположена перед нами по фронту), П - профильной плоскостью проекций (расположена в профиль по отношению к наблюдателю), A - горизонтальная проекция точки А , А - фронтальная проекция точки А , А - профильная проекция точки А .

Оси OX , OY , OZ называются осями проекций. Они аналогич­ны координатным осям декартовой системы координат с той лишь разницей, что ось ОХ имеет положительное направление не впра­во, а влево. Теперь, чтобы получить проекции в одной плоскости (плоскости чертежа), необходимо и профильную плоскость про­екций развернуть до совмещения с фронтальной. Для этого ее нужно развернуть на 90° вокруг оси OZ , причем переднюю полу плоскости развернем вправо, а заднюю влево. В результате получим трехкартинный комплексный чертеж (эпюр Монжа), показанный на рис 1.5, б. Так как ось OY разворачивается вместе с двумя плоскостями П и П , то на комплексном чертеже ее изобра­жают дважды.

Исходя из рис. 1.5, а , очевидно, что А А = OA = А А . Из этого следует важное правило взаимосвязи проекций: расстояние от го­ризонтальной проекции точки до оси равно расстоянию от профильной проекции точки до оси . Тогда по двум любым про­екциям точки можно построить третью. Горизонтальную и фрон­тальную проекции точки А связывает вертикальная линия связи, а фронтальную и профильную проекции – горизонтальная.

В связи с тем, что комплексный чертеж представляет собой свер­нутую в плоскость модель пространства, на нем нельзя изобра­зить проецируемую точку (за исключением случаев, когда ее по­ложение совпадает с одной из проекций). На комплексном черте­же мы оперируем не самими геометрическими объектами, а их проекциями.

Выше было показано, что две проекции точки определяют ее положение в про­странстве. Так как каждая фигура или тело представляет собой совокупность то­чек, то можно утверждать, что и две орто­гональные проекции предмета (при нали­чии буквенных обозначений) вполне опре­деляют его форму.

Однако в практике для изображения изделий, машин и различных инженерных конструкций возникает необ­ходимость в создании дополнительных проекций. Поступают так с единственной целью — сделать проекционный чертеж более ясным, удобочитаемым.

Модель трех плоскостей проекций пока­зана на рис. 1.6, а . Третья плоскость, перпендикулярная П и П , обозначается бук­вой П и называется профильной. Проекции точек на эту плоскость будут также именоваться профильными.

Плоскости проекций, попарно пересека­ясь, определяют три оси: OX , OY , OZ , которые можно рассматривать как систе­му прямоугольных декартовых координат в пространстве с началом в точке О. Три плоскости проекций делят про­странство на восемь трехгранных углов — это так называемые октанты.

Как и прежде, будем считать, что зри­тель, рассматривающий предмет, находится в первом октанте.

Д

ля получения эпюра плоскости Пи вращают, как показано на рис. 1.6, , до совмещения с плоскостью . В результа­те вращения передняя полуплоскость оказывается совмещенной с нижней по­луплоскостью , а задняя полуплоскость — с верхней полуплоскостью . При повороте на 90° вокруг оси передняя полуплоскость совместится с правой полуплоскостью , а задняя полупло­скость — с левой полуплоскостью .

Окончательный вид всех совмещенных плоскостей проекций дан на рис. 1.6, . На этом чертеже оси и лежащие в неподвижной плоскости , изображены только один раз, а ось показана дваж­ды. Объясняется это тем, что, вращаясь с плоскостью , ось на эпюре совме­щается с осью а вращаясь вместе с плоскостью , эта же ось совмещается с осью .