Точки общего и частных положений. Точки проекций общего и частного положения

Точки общего и частных положений. Точки проекций общего и частного положения

Вверх

Наиболее удобной для фиксирования положения геометрической фигуры в пространстве является декартова система координат, состоящая из трех взаимно перпендикулярных плоскостей:

П₁– горизонтальная плоскость проекций;

П₂– фронтальная плоскость проекций;

П₃– профильная плоскость проекций;

Ось х – ось абсцисс;

Ось у – ось ординат;

Ось z – ось аппликат;

О – начало координат.

Положительными направлениями оси считают: дял оси х – влево от начала координат, для оси у – в стороны зрителя от плоскости П₂, для оси z – вверх от плоскости П₁, противоположные направления осей считаются отрицательными (рис. 1.14.).

Рис. 1.14.

Плоскости проекции делят пространство на 8 частей – октантов, каждый из которых представляет собой прямоугольный треугольник, где гранями являются части плоскостей проекций, а ребрами – оси координат.

Учитывая при отсчете координат направления осей х, у, z, получим знаки координат для каждого октанта (табл. 2).

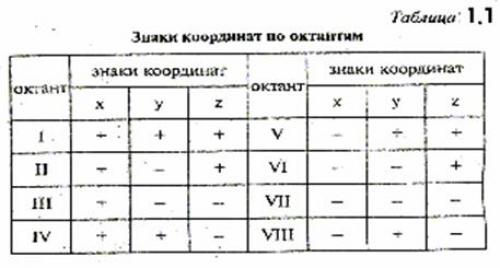
Возможны следующие случаи.

Точка расположена в пространстве. В этом случае ее зададут тремя координатами (измерениями). Все три проекции точки удалены от осей проекций (рис. 1.9.).

Точка находится на одной из плоскостей проекций – П₁, П₂или П₃. В этом случае ее задают двумя действующими координатами, не равными нулю. Одна проекция совпадает с самой точкой, а две другие лежат на осях. На рисунке 1.10. изображены проекции точки В (20, 0, 15), лежащей в плоскости проекций П₂. В этом случае фронтальная проекция В₂совпадает с самой точкой В, горизонтальная проекция В₁лежит на оси Ох, а профильная В₃– на оси Оz.

Точка находится на одной из осей проекций – Ох, Оу, Оz. В этом случае ее задают одной действительной координатой, не равной нулю. Две проекции совпадают с самой точкой, а третья находится в точки О – начале осей проекций. На рисунке 10 изображены проекции точки С (15, 0, 0), лежащей на оси Ох. В этом случае горизонтальная С₁и фронтальная С₂проекции совпадают с самой точкой С, а профильная проекция С₃находится в точке О.

К чтению чертежа следует отнести решение таких вопросов:

а) определение третьей проекции точки по двум данным;

б) определение координат точки и ее положения относительно плоскостей проекции;

в) построение аксонометрического изображения точки по ее комплексному чертежу;

г) анализ взаимного расположения нескольких точек относительно плоскостей проекции и др.

Рис. 1.15.

На рисунке 1.15. заданы проекции точки А и В. Эти точки расположены в пространстве, так как ни одна из их координат не равна нулю. Широта точки А больше широты точки В, так как отрезок ОА_хбольше отрезка ОВ_х. Следовательно, точка А дальше отстоит от плоскости П₃, чем точка В. Глубины этих точек равны вследствие равенства координат у (А₁А_х= В₁В_х). Из этого следует, что точки одинаково удалены от плоскости проекции П₂. Высоты у точек различны. Точка В дальше от плоскости П₁на величину, равную отрезку В₂В₀.

Прямая общего положения. Прямая линия. Способы графического задания прямой линии.

Прямая линия - одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

Классификация прямых

В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

Рисунок 1. Прямая общего положения.

Эпюрный признак прямой общего положения: проекции прямой не параллельны осям проекций (x,y,z)

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются . В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:

2.1. Прямые параллельные горизонтальной плоскости проекций называются или (рис.2). На горизонтальную плоскость проекций они проецируются в натуральную величину..

Эпюрный признак

или (рис.). Эпюрный признак

(рис.4).Эпюрный признак

Прямая перпендикулярная одной плоскости проекций, параллельна двум другим.  В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:

3.1. прямая - .рис.( 5)

3.2. Профильно проецирующая прямая - АВ (рис.6)

прямая - АВ (рис.7)

Если точка принадлежит прямой, то её проекции принадлежат одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке 8 точек, только одна точка С лежит на прямой , так как отвечает требованиям аксиомы.

Конкурирующие точки. Определение видимости в начертательной геометрии с примерами

Определение видимости:

Точки, расположенные на одной проецирующей прямой, называются конкурирующими.

Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).

Рис. 7.1. Конкурирующие точки: а - относительно горизонтальной плоскости проекций;б - относительно фронтальной плоскости проекций

Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D - невидима).

Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).

Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже: а - относительно горизонтальной плоскости проекций;б - относительно фронтальной плоскости проекций

Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П₁, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П₁, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П₁

Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П₂.

Точка общего положения принадлежит. Взаимное расположение точки, прямых и плоскостей с примерами

Взаимное расположение точки и прямой:

Возможны два варианта расположения точки относительно прямой:

• - точка принадлежит прямой (рис. 3.1 а), тогда ее проекции на КЧ лежат на одноименных проекциях прямой.
• - точка не принадлежит прямой (рис. 3.1 б), если хотя бы одна из проекций точки не принадлежит проекции прямой

Взаимное расположение прямых

Прямые в пространстве могут занимать друг к другу одно из трех положений:

• - быть параллельными;
• - пересекаться;
• - скрещиваться.

Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.

Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.

У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А . Причем фронтальная и горизонтальная проекции этой точки должны находиться на одной линии связи.

Рис. 3.3

Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.

Рис. 3.4

Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.

На рис. 3.4 точка С принадлежит прямой b , а точка D на прямой   а . Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций.

Плоскость. Способы ее задания, положение относительно плоскостей проекций

Положение плоскости в пространстве может быть однозначно определено:

• - тремя точками, не лежащими на одной прямой;
• - прямой и точкой, не лежащей на этой прямой;
• - двумя параллельными прямыми;
• - двумя пересекающимися прямыми;
• - плоской фигурой;
• - следом плоскости.

След плоскости – это линия пересечения заданной плоскости с одной из плоскостей проекций.

Соответственно различают горизонтальный, фронтальный и профильный следы плоскости.

Плоскостью общего положения называется плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций.

Плоскостями частного положения относительно плоскостей проекций называются плоскости параллельные или перпендикулярные им.

Плоскость перпендикулярная одной из плоскостей проекций называется проецирующей плоскостью.

Существует три вида проецирующих плоскостей: горизонтально- проецирующая, фронтально-проецирующая и профильно-проецирующая плоскости. Такие плоскости вырождаются в прямую линию (след плоскости) на ту плоскость проекций, к которой они перпендикулярны.

1. Горизонтально-проецирующая плоскость  - плоскость перпендикулярная горизонтальной плоскости проекций.

2. Фронтально-проецирующая плоскость – плоскость перпендикулярная фронтальной плоскости проекций.

3. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня.

Существует три вида плоскостей уровня: горизонтальная, фронтальная и профильная плоскости уровня.

1. Горизонтальная плоскость – плоскость, параллельная горизонтальной плоскости проекций.

2. Фронтальная плоскость  - плоскость, параллельная фронтальной плоскости проекций.

Точка частного положения это. Взаимное положение двух точек. Условия видимости на чер­теже

Рассмотрим чертеж модели, изображенной на рис. 3.6. Проекции некоторых точек совпадают, так как они расположены на одной проецирующей прямой. Например, на горизонтальной плоскости совпали проекции а и b вершин А и В - они лежат на одной горизонтально - проецирующей прямой. На фронтальной плоскости совпали проекции с ' и d ' вершин С и D - они лежат на одной фронтально-проецирующей прямой.

Точки, лежащие на одной проецирующей прямой, называют конкурирующими . А и В - горизонтально-конкурирующие точки, а С и D - фронтально-конкурирующие точки и т.д.

Ясно, что если две точки лежат на одной проецирующей прямой, то одна из них закрывает другую. Как определить, какая из них будет видимая и какая невидимая?

Из двух горизонтально- конкурирующих точек на горизонтальной плоскости видима та, которая расположена в пространстве выше. Анализируя положение фронтальных проекций точек (рис. 3.7), определяем, что точка А имеет большую координату z, чем точка В.

Следовательно, точка А расположена выше точки В и при проецировании на горизонтальную плоскость проекций закроет точку В. Точка А на горизонтальной плоскости видима, точка В - невидима. На фронтальной плоскости они обе видимы.

Из двух фронтально- конкурирующих точек на фронтальной плоскости проекций будет видима та, которая расположена ближе к наблюдателю, стоящему лицом к фронтальной плоскости проекций (рис. 3.8).

Какая из точек ближе к на­блюдателю, можно определить по горизонтальным проекциям. Например, сравнивая горизонтальные проекции точек D и С , заключаем, что на фронтальной плоскости проекций видима точка С, а точка D - невидима, так как

Из двух профильно-конкурирующих точек на профильной плоскости проекций бу­дет видима та точка, которая расположена левее.

Итак, если на чертеже одноименные проекции точек не совпадают или совпадает только одна пара проекций, то такие точки в пространстве не совпадают, а удалены друг от друга на определенное расстояние (рис. 3.7, 3.8).